There are 7 important terms of waves that form the foundation for understanding waves. Besides, the wave speed equation describes how waves behave.

Introduction

Not only physics but also engineering disciplines such as civil engineering, electronic engineering, and mechanical engineering rely on wave principles. The waves are all around you, for instance:

the sound of your voice
the vibration of a guitar string
the ripples spreading across a pond
the invisible electromagnetic signals

Illustration of Language of Waves _ A Beginner's Guide

If you are beginning your journey into the world of waves, learning the basic terminology and formulas is essential. Think of this as your quick-reference guide:

“The language of waves and the mathematics that describes them”.

Key Terms in Wave Physics

Before working with wave equations, it is important to understand the basic vocabulary of waves. These terms form the foundation for analysing all types of waves, including:

Mechanical Waves
Electromagnetic Waves

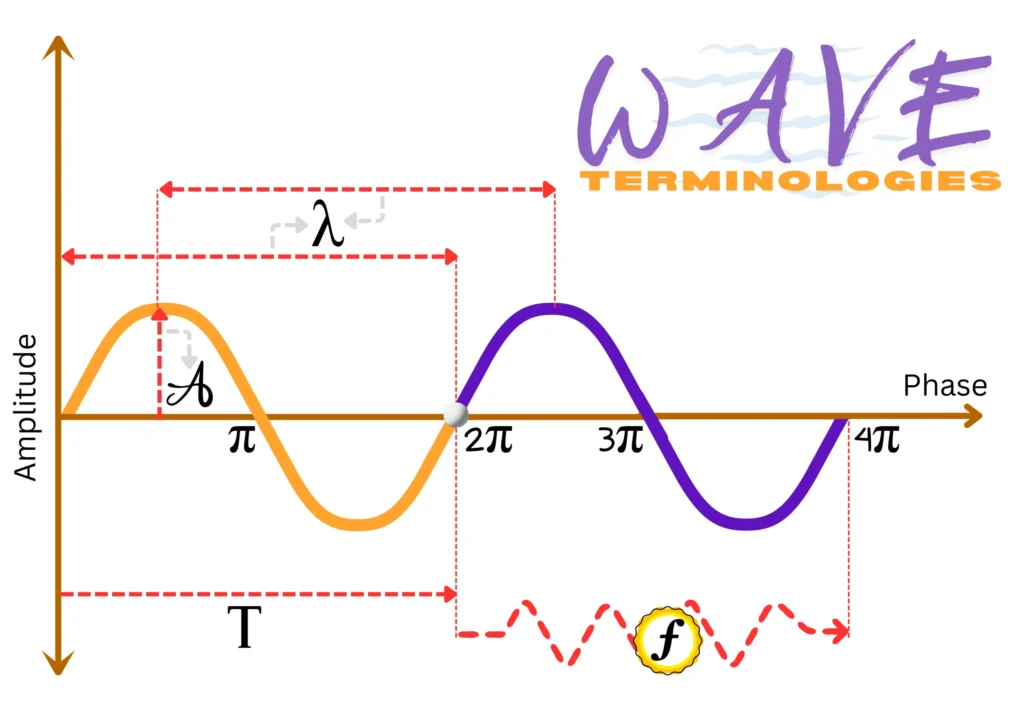
1. Amplitude (A)

The maximum displacement of a particle from its equilibrium (rest) position. A larger amplitude means the wave carries more energy.

2. Wavelength (λ)

The distance between two consecutive points that are in the same phase, such as crest-to-crest or trough-to-trough. Its SI unit is the meter (m).

3. Frequency (f)

The number of complete waves (oscillations or cycles) that pass a point in one second. The SI unit is hertz (Hz), which is equal to cycles per second.

4. Period (T)

The time taken for one complete oscillation of the wave to pass a point. It is measured in seconds (s). Frequency and period are inversely related:

$f = \frac{1}{T}, \quad T = \frac{1}{f}$

5. Medium

The material through which a wave propagates is called a medium.

Mechanical waves (like sound or water waves) require a medium such as air, water, or a string, while electromagnetic waves (like microwave, visible light, or radio waves) can travel through a vacuum.

6. Wavefront

A wavefront is a surface that connects all points of a wave vibrating in the same phase. In simple terms, every point on a wavefront is “doing the same thing” at the same time (all crests together, all troughs together).

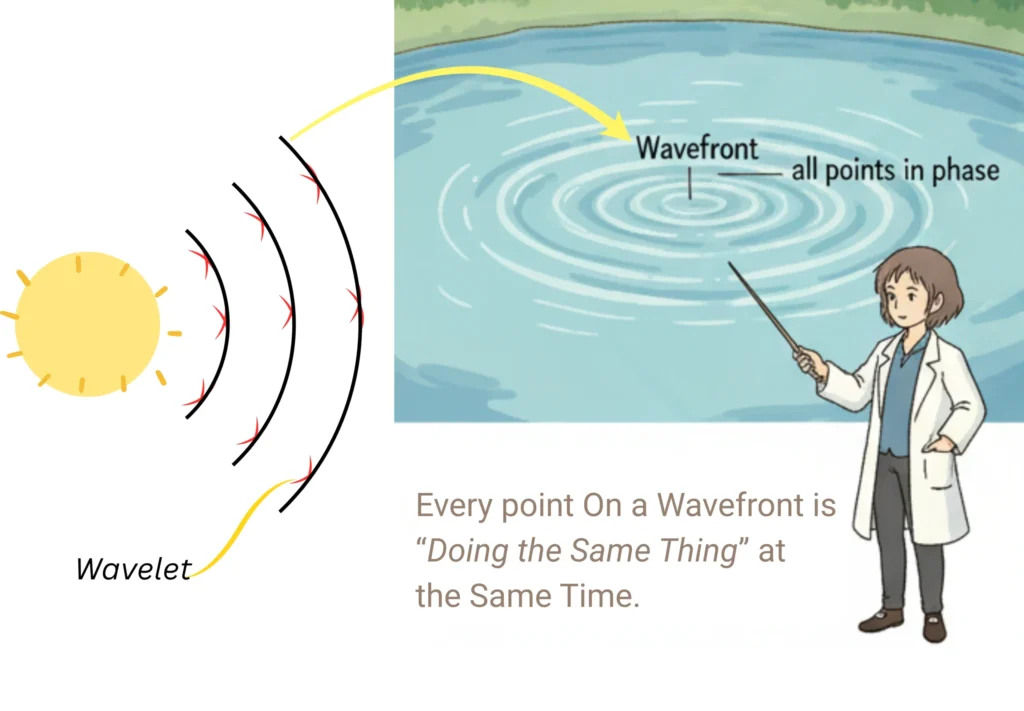
Illustration of Wavefronts and Wavelets in Wave Physics

Note

According to Huygens’ Principle, every point on a wavefront can be treated as a source of tiny secondary waves called wavelets. The new wavefront at a later time is formed by drawing the outer boundary (envelope) of all these wavelets.

7. Phase (φ)

Phase is a measure of how far a point has progressed through its wave cycle. It tells us the “stage” of vibration at a given time and position.

In-Phase

Two points are said to be in-phase if they are at the same stage of vibration (for example, both at a crest or both at equilibrium moving upward).

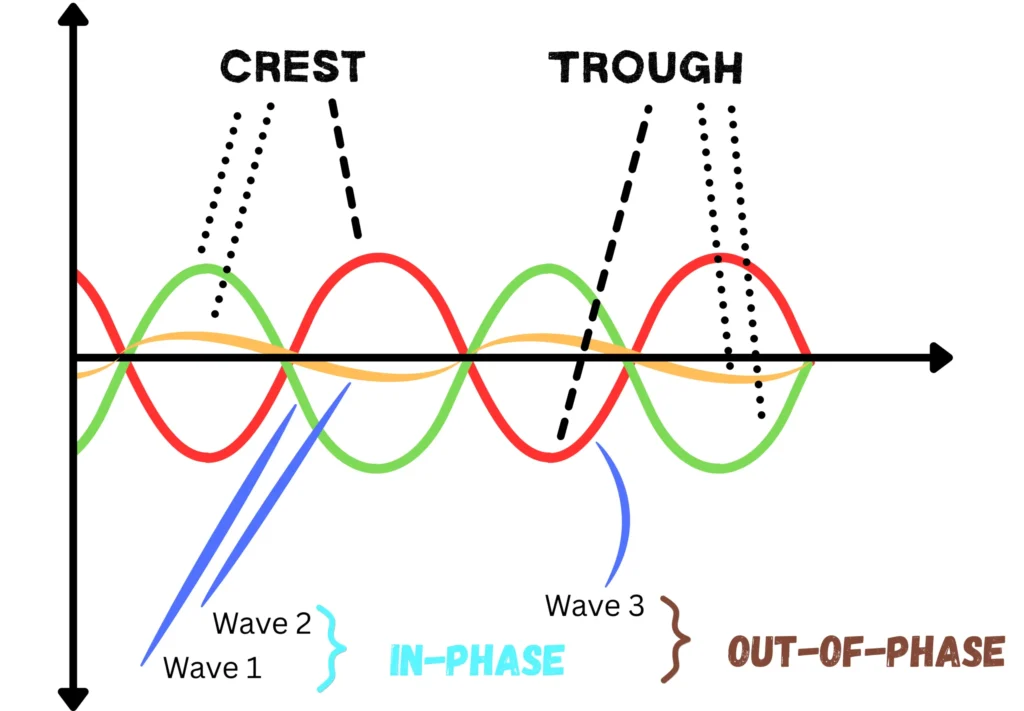
Out-of-Phase

Two points are out of phase if their vibrations are not synchronised. The most extreme case is when one is at a crest while the other is at a trough.

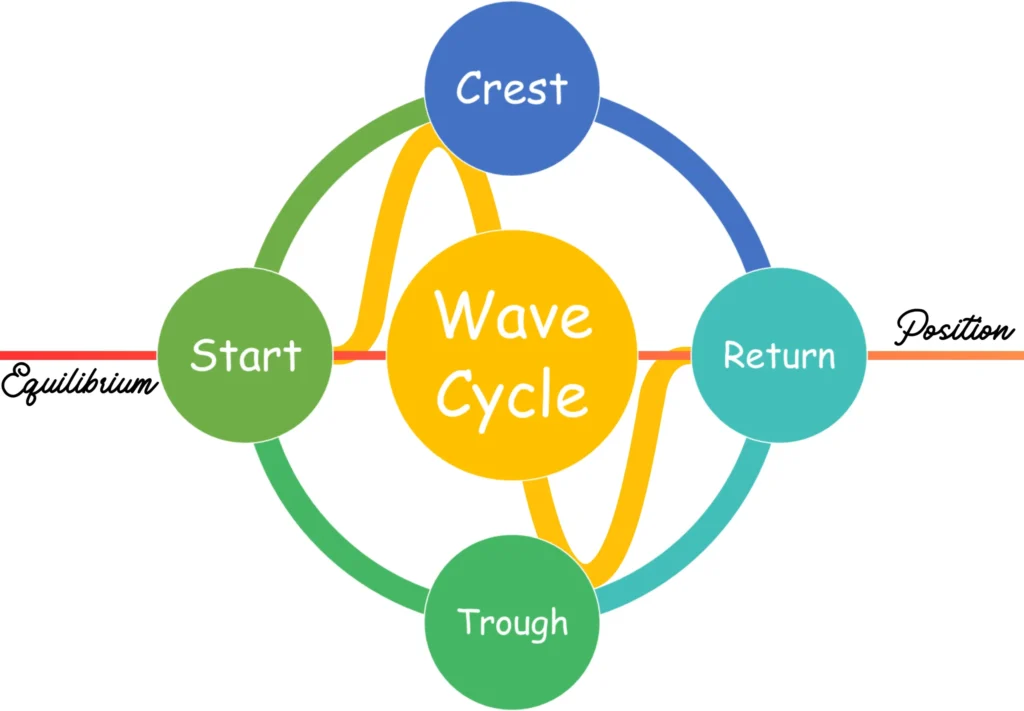
Wave Cycle

A wave cycle is one complete pattern of a wave. After this, the wave repeats itself. For a sine wave, a full cycle is:

Transverse Waves vs Longitudinal Waves

Feature	Transverse Waves	Longitudinal Waves
Particle Motion	Particles oscillate perpendicular to the direction of wave propagation.	Particles oscillate parallel to the direction of wave propagation.
Direction of Energy Transfer	Energy travels at right angles to particle motion.	Energy travels in the same direction as particle motion.
Examples	– Light Waves – Water Surface Waves – Waves On A String	– Sound Waves In Air – Compression Waves In Springs
Anatomy	– Crest: the highest point of the wave. – Trough: the lowest point of the wave.	– Compression: region where particles are close together (high pressure). – Rarefaction: region where particles are spread apart (low pressure).
Medium Requirement	It can propagate in solids and on surfaces. Electromagnetic transverse waves can also travel in a vacuum.	It requires a material medium (solid, liquid, or gas). Cannot travel in a vacuum.

Illustration of Trasverse Wave vs Longitudnal Wave

Wave Speed Equation

It is the most fundamental formula for waves.

This equation ties together how fast a wave moves, how frequently it oscillates, and the spacing between its crests.

Now, consider a transverse wave as shown below.

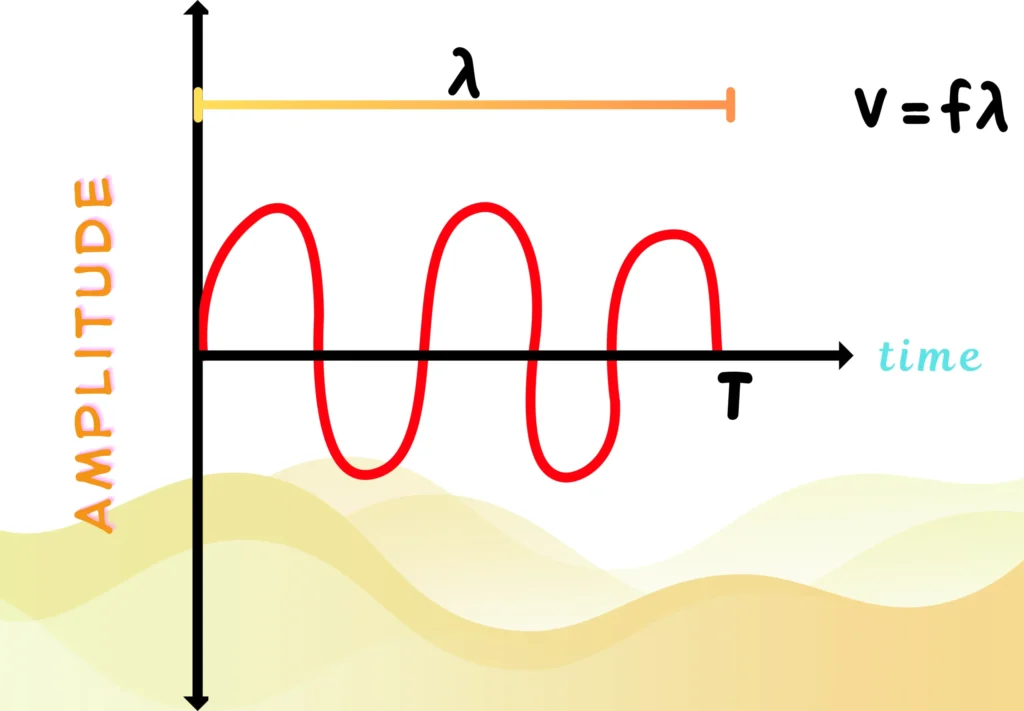
Illustration of Transverse Wave for the Derivation of Wave-Speed Equation

Let!

Total Distance Covered by the Wave (Wavelength) = $\lambda$
Toatl Time Taken by the Wave (Period) = $T$

According to definition of speed $\left(v\right)$ :

$v = \frac{\text{distance}}{\text{time}}$

$v = \frac{\lambda}{T}$

From the definition of period (T):

$f = \frac{1}{T}$

Hence,

$v = f \lambda$

Where:

$f = \text{frequency} \left(Hz\right)$

Why This Matters?

Understanding these terms and formulas helps you:

Make sense of ripple tank experiments and sound wave studies.
Connect simple harmonic motion (like pendulums or springs) to real-world wave phenomena.
Build a strong foundation for advanced topics like standing waves, resonance, and electromagnetic waves.

Conclusion

Waves may appear abstract at first, but they follow a clear language of terms and equations. These basics are the foundation for understanding how waves shape the world around us. From the simple to the complex, the same principles explain:

Vibrations in a string that produce sound and music.
Ripples in water that spread outward from a disturbance.
Signals traveling through space that power communication and modern technology.

Mastering these fundamentals is the first step toward exploring the deeper and more advanced concepts of wave physics.

Frequently Asked Questions (FAQs)

What are the 7 important terms of waves?

The seven key terms of waves are amplitude, wavelength, frequency, period, wavefront, phase, and medium. These terms form the foundation for understanding all types of waves.

What is the basic equation of wave speed?

The fundamental wave speed equation is:

$v = f \lambda$

where v is wave speed, f is frequency, and λ is wavelength.

What is the difference between transverse and longitudinal waves?

Transverse Waves: particles oscillate perpendicular to the direction of propagation (e.g., light, water waves).
Longitudinal Waves: particles oscillate parallel to the direction of propagation (e.g., sound waves).

What are wavefronts and wavelets?

A wavefront is a surface connecting all points in the same phase of vibration. According to Huygens’ Principle, each point on a wavefront acts as a source of small secondary waves called wavelets.

What does in-phase and out-of-phase mean in waves?

In-phase: two points vibrate in the same stage of the cycle (e.g., crest to crest).
Out-of-phase: two points vibrate in opposite stages, like a crest and a trough.

What is the difference between compression and rarefaction in sound waves?

Compression: a region where particles are close together, creating high pressure.
Rarefaction: a region where particles are spread apart, creating low pressure.

Why are wave equations important in physics?

Wave equations like $v = f \lambda$ help calculate how fast waves travel, how often they oscillate, and how far apart wave crests are. It is essential for studying sound, light, and electromagnetic signals.

How are waves used in real life?

They are used in sonar, optical fibres, wireless communication, medical imaging, and noise-cancelling headphones. They also explain natural phenomena like ripples in water and vibrations in strings.

7 Important Terms of Waves and the Basic Wave Speed Equation You Must Know

Table of Contents