Embark on a journey through the fascinating world of numbers to learn about place value and numeric representations of a number. Here, we shall explore the mysteries of the specific place of each digit in a number, decode the difference between numbers in words and the normal form of a number, and untie the secrets of expanded form.
Table of Contents
Introduction
What is the big deal with the specific location of a number, also called place value, and numeric representation? How does knowing these specific places and numeric representations help us play with numbers and solve tricky math problems? Well, this is the focus of this discussion.
Place Value
When you started your education, you were introduced to the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Understanding these digits is the first step in learning about numbers. The next phase is to explore the concept of place value. It can be defined as “the special value of a digit based on its position within a number.”
Note! These values are always read from right to left, and these are:

How to Determine a Place Value?
Imagine yourself standing in front of a mysterious locked door, and you are told that the code of the chest is “9125.” But to open the door, you have to enter each digit of the secret code in a specific place. “Goodness gracious!?”
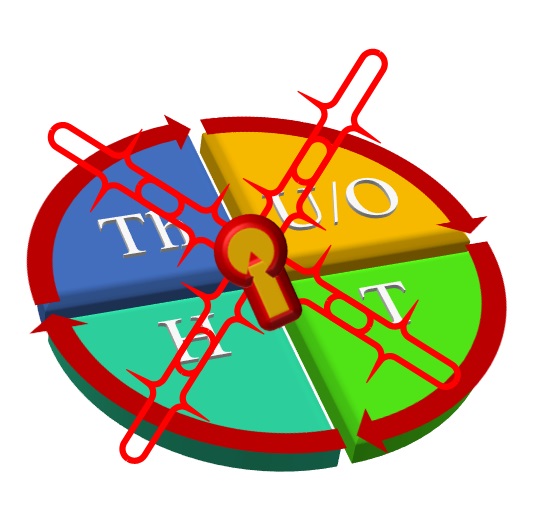
Since you are convinced there is something incredible inside, you are feeling ticklish all over, but you cannot figure out how to open it. This shows that numbers hold so much power and mystery that understanding them sometimes feels like cracking a secret code.
But there is no need to worry! We shall be solving this mystery real soon!
Let us break down this example, i.e., “9125.” Each digit in this number has a special position. Point to ponder! There can be as many places as there are digits; however, for the given example (9125), there are only four of these places. They are represented as:
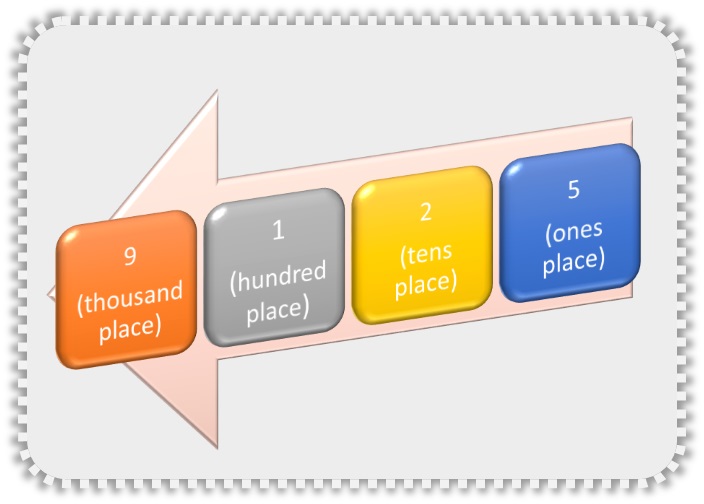
Did you notice? There are 9 thousands (Th), 1 hundred (H), 2 tens (T—read as twenty), and 5 ones (O/U—read as five). Voila! We have discovered the secret identity of the mysterious door, which is “9 in the thousand place, 1 in the hundred place, 2 in the tens place, and 5 in the ones place.”

Ding Dong! We are eligible to unlock the true power of numbers by decoding their respective places and solving all kinds of math puzzles. So get ready, put on a “math superhero” cloak, and start decoding secret codes called place values!
Points to Ponder for Place Value and Numeric Representation
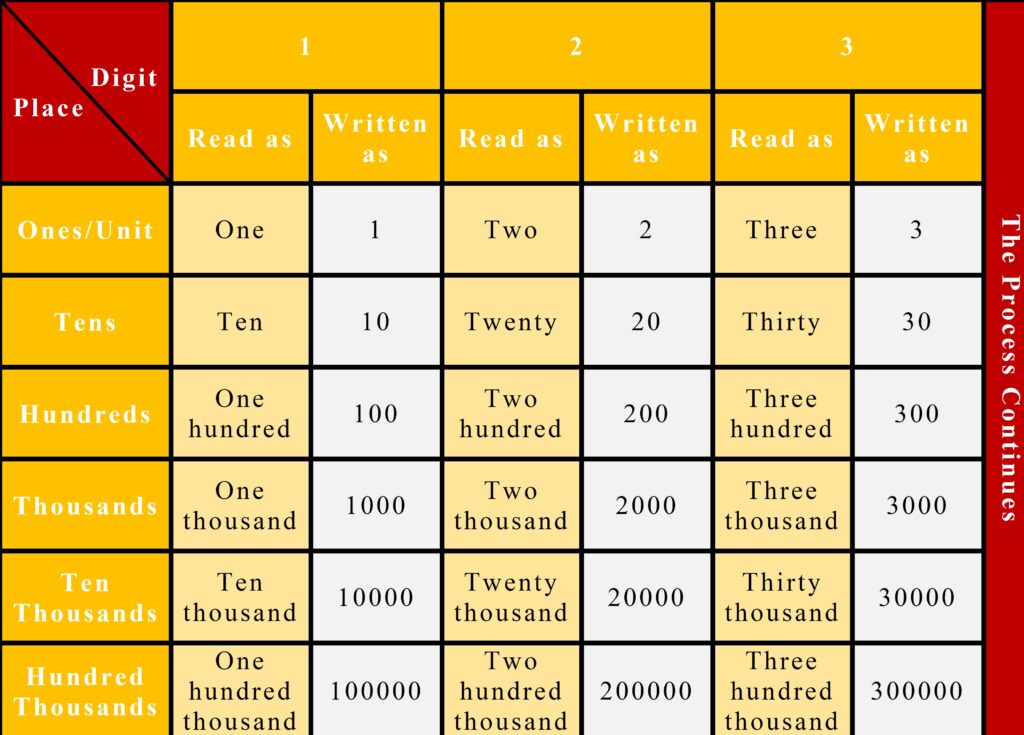
The below table shows how to read and write digits corresponding to their places in a number.
Verbal and Standard Number Forms
A number can be like a secret code or a colorful picture. For instance, when we use words to talk about numbers, it is like describing the picture on a puzzle piece. But when we write numbers using digits (1, 2, 3, etc.), it is like putting all the puzzle pieces together to see the whole picture.
Now coming towards the main course, “What is the difference between verbal and standard form?” Well!
The former refers to the representation of a number in words, whereas the latter refers to the representation of the number in digits (numeric notation).

Numeric Notation to Words
For example, if we want to write the number 256 in words, we first need to know about its places, which are:

In this number, there are 2 hundreds, 5 tens (read as fifty), and 6 ones (read as six), hence, the number is called “two hundred fifty-six.”
Let us consider a bit more complex number, like “36709.” Did you notice? Now there are a total of five digits in the number. Also, each digit has its own special place, which is:

Here, we have 3 ten thousands (3 ten is read as thirty), 6 thousands, 7 hundreds, 0 tens (meaning no value of tens), and 9 ones (read as nine). Well, based on this, the number could be read as:
- thirty thousand six thousand seven hundred zero nine ×
- thirty-six thousand seven hundred nine «
- thirty-six thousand seven hundred and nine «
Comparing these statements, we can say that the first statement is entirely wrong. On the other hand, we would say that the second statement is correct but not grammatically accurate. However, the third statement is not only correct but also grammatically accurate. It is because:
- A place with a zero digit is not mentioned.
- The repetition of a place name is not allowed.
- The word “and” is added after the hundred-place name.
Words to Numeric Notation
Well, what will happen if we have to do the reverse? For such a case, let us take a number, for example, “one hundred and ninety-two.” There are three places in this number. How do we know about it?
Actually, it is pretty simple. The hundred in the number indicates that there are at most three places. So, just collect the shattering pieces of the number as shown in the figure.
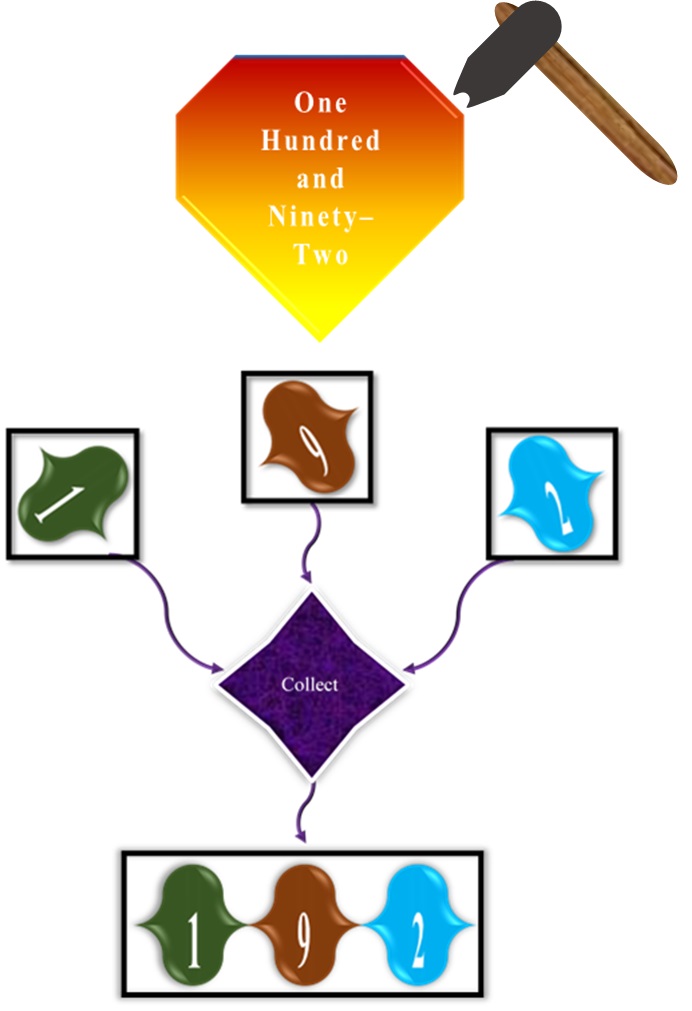
Cool! We have learnt about converting a number from words to numeric notation, and it is 192.
Now, a bit more complex number like “seven hundred and two thousand and fifty-two.” Since there is thousand in the number, so for such a number, we shall consider the section before (to the left) and after (to the right) the “thousand” as shown in the figure.
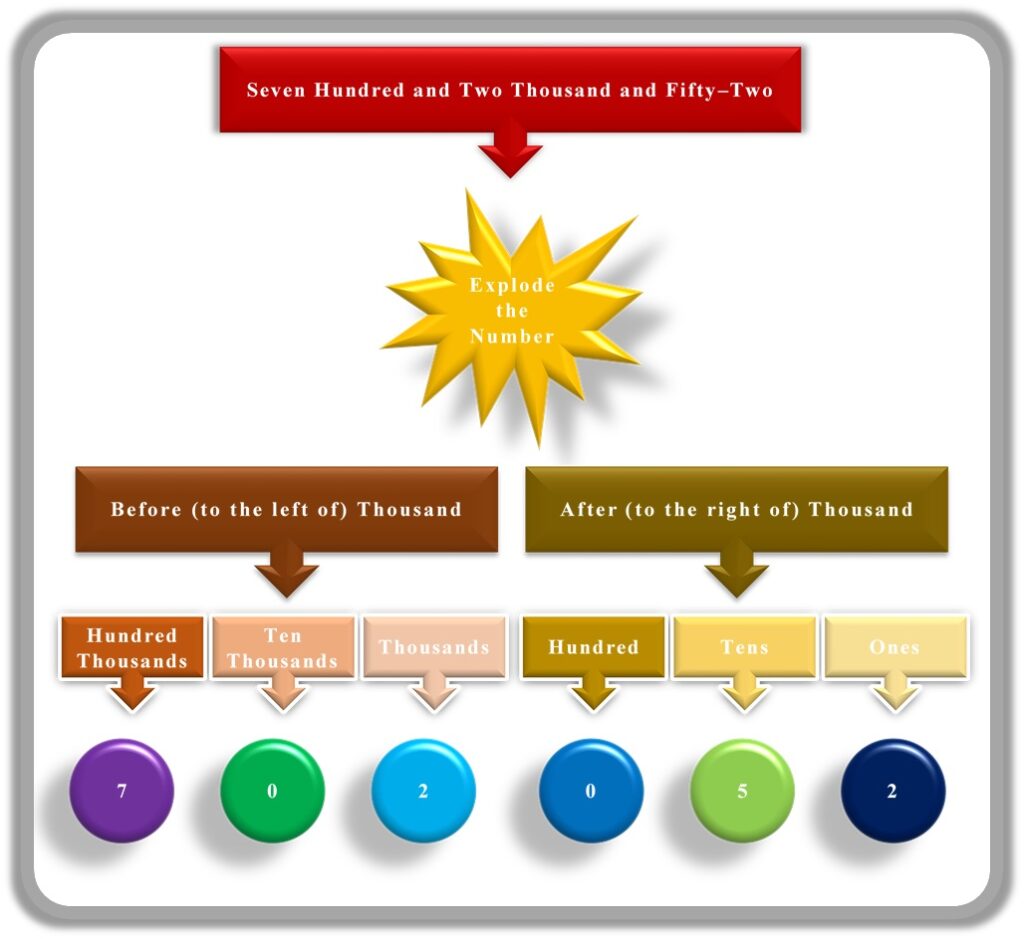
There are six places in the number, and out of the six, two places are missing (meaning 0). So, for the numeric notation of the number, all we need to do is consider:
- digits before thousand as a regular three-digit number
- digits after thousand as a separate three-digit number
Hence, we got our number, and it is “702 052.” Was it that hard? Nah! It was simple. In the end, just keep the following points in mind and we are good to go.
- Boom! Explode the numbers before and after the thousand.
- Write 0 in the position of a missing place.
Why the Different Forms?
Now the question is, why are we bothering ourselves with verbal and numeric forms of numbers?
Well, in our everyday lives, when we communicate with others, we often speak numbers in words. It helps us communicate more clearly in various situations.
On the contrary, when we are shopping at the grocery store, calculating distances for a road trip, or keeping track of scores in sports, we prefer to write them down in numeric notation rather than in words.
This is the reason we have two different forms of numbers to represent them.
Since we have reached here, it is time to become a detective. Just hold your pocket mirror and sharpen your detective skills by looking at different numbers and finding out their verbal and standard numeric form.
Expanded Form vs. Standard Form
Sometimes, we want to see each part of the puzzle separately. It is like looking at individual puzzle pieces. Writing a number in expanded form is akin to this, where each digit gets its own spotlight.
But other times, we want to see the whole puzzle completed. It is like putting all the pieces together to see the complete puzzle. This is like writing a number in standard form (also called the normal form of a number), where all the digits come together to form the complete picture.

Expanded Form
Imagine we have the number 427. It might seem like just a string of digits, but each digit has a special role to play, which depends upon its place. Let us break down these places to understand the given number more properly:

When we put these pieces together, we get 400 + 20 + 7, the expanded version of a number. If we add these, we shall get 427.

This indicates how the expanded version of the number works. It is like taking shuffled pieces of a puzzle and examining each piece before putting it back together again with a magical wand.
So, what will happen if we have a number like 320192? Can you guess the way this number looks when expanded? Yes! Upon observing closely, we shall notice that there are six places:
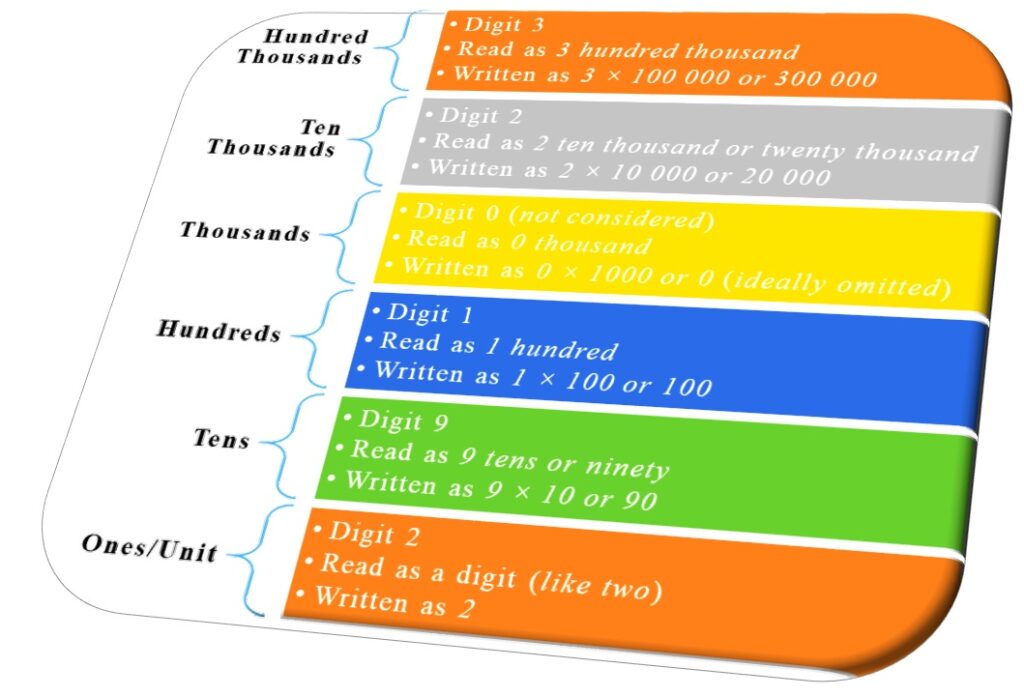
So, the expanded version of this number is represented as 300000 + 20000 + 0 + 100 + 90 + 2, or more preferably, it would be written as 300000 + 20000 + 100 + 90 + 2.
Why do we do it like this? The answer is, if we look at the number closely, there is no hundred. So, in the number, the value of a hundred places is omitted to represent it in the most simplified form.
Standard (Normal) Form
So far, we have seen the conversion of a number from expanded to its normal form. Now, we shall learn about the reverse scenario.
Take the expanded version of a number, for instance, 700 + 50 + 4, and we are asked to convert it to the normal form. The steps involved in writing it in the standard form are:
- Firstly, write the expanded number.
- Secondly, write the total number of digits in every number.
- Thirdly, determine the place for each number (digit) and combine it.

Since there is no missing place value, the standard form of the number would simply be written as 754.
Now, for a bit of a complex number in the expanded state, say 900000 + 20000 + 10 + 9, we are asked to convert it into a normal form. All the steps involved in doing so are the same, and these are:
- Firstly, write the expanded version of the numbers.
- Secondly, write the total number of digits in every number.
- Thirdly, determine the place for each number and combine it.
There is one more step, and it is:
- Fourthly, identify both zero and non-zero place values by reviewing the number.
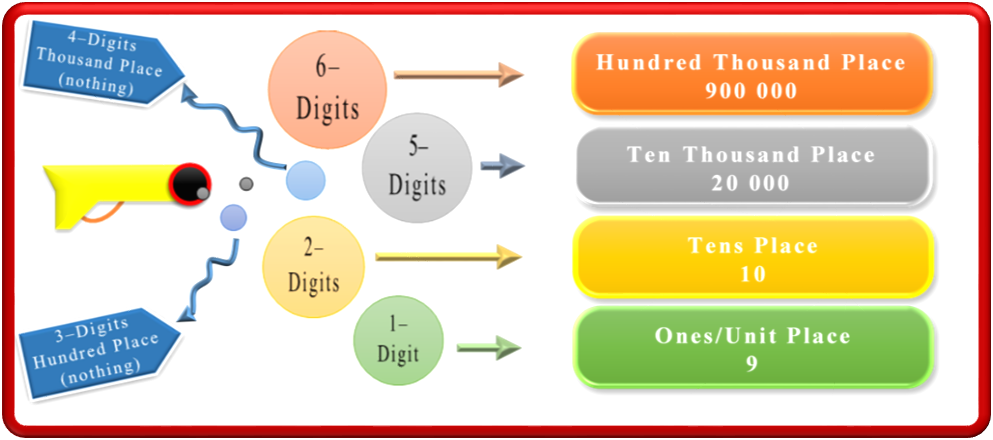
Only the two place values are zero, which are thousand and hundred. Hence, the number 900000 + 20000 + 10 + 9 can be further expanded, like 900000 + 20000 + 0 + 0 + 10 + 9, and the normal form of the number is 920019.
By learning how to break numbers into their place values and then put them back together, we become master puzzle solvers. So, get ready to explore the world of expanded form and standard form.
Conclusion
Wow, what an incredible journey we have had so far while exploring the fascinating world of place value! We have explored the mysteries of numbers, unlocked their hidden power, and discovered the magic of place value.
We also witness how numbers are expressed in numeric notation as well as in verbal form. Not only this, but we also learnt the difference between the expanded form of a number and the standard (or normal) form of a number.
Now, a big round of applause for your hard work, curiosity, and dedication to mastering the secrets of numbers.
Remember this: place values and numeric representation are just the beginning of an incredible adventure in the world of mathematics. So, it is important to keep on exploring and learning new things and embrace the wonders of mathematics.
Whether we are solving puzzles, sorting out mysteries, or embarking on new adventures, remember that we are all math-e-magicians in the making. With this newly acquired knowledge and skills, we are ready to conquer any challenge that comes our way.
Congratulations, math wizard! May your future adventures be filled with endless discovery and excitement! So, I leave you with this: chase your dreams and never stop.
Frequently Asked Questions (FAQs)
What is place value, and why is it important?
Place value can be defined as “the value of a digit based on its position within a number.” It is important because it helps us understand the impact of each digit in a number and how it contributes to its overall value.
How do we read numbers aloud using place value?
Reading numbers aloud involves two steps. In the first step, the place value of each digit is identified. In the second step, starting from the leftmost digit, the value of each place is stated.
For example, in the number 325, the digit 3 is in the hundreds place, 2 is in the tens place, and 5 is in the ones place, so we say “three hundred and twenty-five.”
What is the difference between the verbal form and the standard form of numbers?
Verbal form refers to stating a number in words, while standard form denotes the number using digits (numeric notation).
For instance, the number “256” in verbal form is “two hundred fifty-six.”
How do we convert numbers from verbal to standard form and vice versa?
To convert from verbal to standard form, we identify the place value of each word and write down the corresponding digits.
Similarly, to convert from standard to verbal form, we break down the digits into their place values and express them in words.
What is the expanded form of a number?
Expanded form refers to the breaking down of a number into pieces and writing them as the summation of its place values.
For example, the number 420 in its expanded form is 400 + 20 + 0.
Why do we need to know about expanded forms?
The expanded form of a number helps us understand the individual value of each digit within a number. It makes it easier to manipulate and work with numbers in different mathematical operations like addition, subtraction, multiplication, and division.
How does understanding place value and numeric representation help us in real life?
Understanding place value and numeric representation is essential in everyday activities like shopping, keeping track of scores in any sport, and understanding measurements. It enables clear communication and efficient problem-solving.
