What are equations of motion? They are fundamental tools in physics that describe the relationship between the position, velocity, acceleration, and time of a moving object.
Table of Contents
Introduction
Equations of motion allow us to predict the motion of an object in the future based on its initial conditions and the forces acting upon it. Whether a person is a student, hobbyist, or professional in physics or engineering, learning these equations can be valuable.
These equations are broken down into three key equations and also called as kinematic equations. These are commonly used in physics to solve problems related to the movement of objects under constant acceleration and make our work easier to understand.
What are Equations of Motion?
These equations describe how an object moves under constant acceleration. They are particularly useful in classical mechanics, where they apply to any object moving in a straight line or along a curved path with constant acceleration.
In simpler terms, if we know a couple of these elements (terms associated with motion, e.g., distance, speed–either initial or final or both, acceleration and time of journey), we can use these equations to figure out where it will be and how fast will it go at any point in time etc.
In this blog, FYI, the symbol v is used for the magnitude of velocity (can be called as speed), and the symbol d is used for the magnitude of displacement (also called as distance, S).
The 3 Equations of Motion
The three equations are applied when acceleration is constant during the motion (shown in the motion-time graph). They relate the four key variables;
- displacement (d),
- initial velocity (vi)
- final velocity (vf)
- acceleration (a)
- time (t)
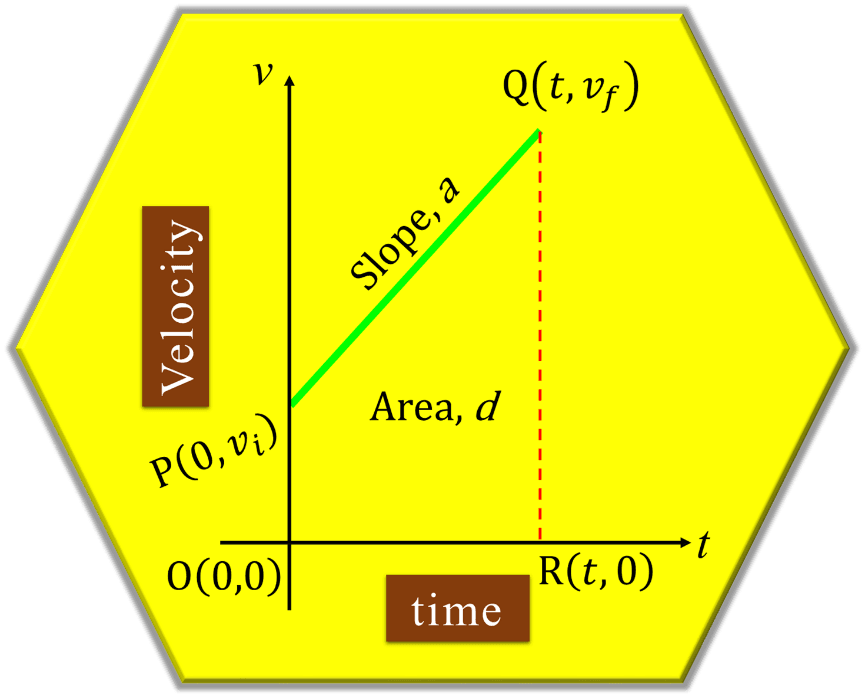
First Equation of Motion
Consider the graph as shown above. To derive the first equation of motion, we will find its slope (m),
![\[slope=\frac{rise}{run}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-e3b8e355c265e367548ec578682f4ed4_l3.png "Rendered by QuickLaTeX.com")
![\[m=\frac{y_2-y_1}{x_2-x_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-6e23eb861d105d91d5f550b5c0ff3c6f_l3.png "Rendered by QuickLaTeX.com")
Since,
![\[Slope=Acceleration\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-c36e85a74e92c68d0450ca62861ce3d2_l3.png "Rendered by QuickLaTeX.com")
![\[a=\frac{v_f-v_i}{t-0}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-95c542069b61d28a5b4d028163962b98_l3.png "Rendered by QuickLaTeX.com")
![\[a=\frac{v_f-v_i}{t}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-bfc9a174aca84b292c6a33c67c3092cd_l3.png "Rendered by QuickLaTeX.com")
![\[at=v_f-v_i\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-f9b45321df7aa98fba3ca05caa2c3c83_l3.png "Rendered by QuickLaTeX.com")
![\[v_f=v_i+at\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-90d0b83c86ef48db7f92f1733b3801a0_l3.png "Rendered by QuickLaTeX.com")
Inference
This equation shows how the final velocity vf depends on the initial velocity vi, the acceleration a, and the time t. It is perfect for calculating how fast something is going after a certain amount of time, assuming constant acceleration.
Second Equation of Motion
Consider the graph as shown above. To derive the second equation of motion, we will find area under the graph line (A),
![\[Area\ under\ Graph\ Line\ \overline{PQ}=Area\ of\ Trapezium\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-644397cf822eb2753f77e1defaa6889c_l3.png "Rendered by QuickLaTeX.com")
![\[A=\frac{1}{2}\left(h_1+h_2\right)b\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-814831868da1e0703a078abae74563f0_l3.png "Rendered by QuickLaTeX.com")
![\[A=\frac{1}{2}\left(\overline{OP}+\overline{RQ}\right)\overline{OR}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-7bb3fde66741416999d1b3e614ba6012_l3.png "Rendered by QuickLaTeX.com")
![\[d=\frac{1}{2}\left(v_i+v_f\right)t\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-7c0f80202fbab7f4237455303f29e5df_l3.png "Rendered by QuickLaTeX.com")
From the first equation of motion.
(Note: Every step till this point is the same for both second and third equation of motion)
Putting value of vf in the last equation.
![\[d=\frac{1}{2}\left(v_i+v_i+at\right)t\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-9f03587fefe4e1671ae763edb95b15f2_l3.png "Rendered by QuickLaTeX.com")
![\[d=\frac{1}{2}\left(2v_i+at\right)t\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-1fdbbca241046548d3c3e222d4790754_l3.png "Rendered by QuickLaTeX.com")
Simplifying,
![\[d=\frac{1}{2}\times2v_i\times t+\frac{1}{2}\times at\times t\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-f5d3bdf57ec238789157e5a483adc5cb_l3.png "Rendered by QuickLaTeX.com")
![\[d=v_it+\frac{1}{2}at^2\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-6a751d9dfc13cf09ee8ff23d18e4b9e9_l3.png "Rendered by QuickLaTeX.com")
OR
![\[S=v_it+\frac{1}{2}at^2\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-e15ae3ff457b6ce6a62d24128c3ee654_l3.png "Rendered by QuickLaTeX.com")
Inference
This equation helps calculate the distance S. In other words, it is useful when we want to know how far an object moves (or has moved) after starting at an initial velocity (vi) and accelerating at a constant rate (a) overtime (t).
Third Equation of Motion
Consider the graph as shown above. To derive the third equation of motion, we will find area under the graph line (A),
(Note: Look for the second equation of motion for previous steps.)
![\[v_f-v_i=at\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-1dcea08cbc1aea8ebddd5e6413620df1_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{\left(v_f-v_i\right)}{a}=t\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-6e97cc7ce6c2c37da96a2f244fd08449_l3.png "Rendered by QuickLaTeX.com")
Putting value of t in the previous equation.
![\[d=\frac{1}{2}\left(v_i+v_f\right)\frac{\left(v_f-v_i\right)}{a}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-61f5ee93af7c4d4fb713a7cb06599b6a_l3.png "Rendered by QuickLaTeX.com")
Simplifying,
![\[d=\frac{1}{2}\left(v_f+v_i\right)\frac{\left(v_f-v_i\right)}{a}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-4d1ea5a2bcbbe432845c5a240cb1ac8a_l3.png "Rendered by QuickLaTeX.com")
![\[d=\frac{\left(v_f^2-v_i^2\right)}{2a}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-741153302f3899f5d3c2ec0dd43edd7e_l3.png "Rendered by QuickLaTeX.com")
![\[2ad={v_f^2}-{v_i^2}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-c789d8c8851b702875d8fed4f49c673f_l3.png "Rendered by QuickLaTeX.com")
OR
![\[2aS={v_f^2}-{v_i^2}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-8cb99a7c31c561f6c9b4283932be2226_l3.png "Rendered by QuickLaTeX.com")
Inference
This equation is handy when we know all the parameters of motion except the time t. It relates the final velocity (vf) to the initial velocity (vi), the acceleration (a), and the distance (S).
Examples of Equations of Motion in Action
Problem 1
A car starts from rest and accelerates uniformly at 2 m/s2. Find the velocity of the car after 5 seconds.
Problem 2
A train is moving with an initial velocity of 36 km/h. It accelerates uniformly at 0.5 m/s2 for 10 seconds. Calculate the distance covered by the train in this time.
Problem 3
A cyclist starts from rest and accelerates uniformly at 1 m/s2 for a certain time. After reaching a velocity of 10 m/s, the cyclist decelerates uniformly at 2 m/s2 until coming to rest. Find the total distance covered by the cyclist.
Why are Equations of Motion Important?
The equations of motion are foundational in physics because they help us understand how objects move, whether they are cars on the road, athletes running on the track, or satellites in the space.
In fields like engineering, mechanics, and aerospace, these equations are crucial for designing systems that rely on precise motion control.
Conclusion
Equations of motion are a powerful tool for solving problems related to linear motion with constant acceleration.
By understanding and applying these three key equations, we can predict the future of moving objects in various scenarios. Whether we are studying physics for school or applying it in our career, these equations will give us insight into the forces that govern motion in the physical world.
Frequently Asked Questions (FAQs)
What are the 3 equations in kinematics?
They are equations that relate displacement, velocity, acceleration, and time in motion under constant acceleration.
When can you use the equations of motion?
When acceleration is constant and the motion is in a straight line.
How does the 1st equation of motion differ from the 3rd?
The first relates velocity to time, while the third connects velocity with displacement, without needing time.
What is displacement in the 2nd equation of motion?
It refers to the distance covered by an object in a specific direction.
Can these equations be used for circular motion?
No, they are primarily for linear motion with constant acceleration.
What is acceleration?
It is the rate at which the velocity of an object changes over time.
How do you calculate final velocity?
It depends upon the parameters provided. However, of the three equations, only two can be used to determine the final velocity. These are 1st and 3rd equations of motion.
What role does time play in these equations?
Time connects velocity and displacement with acceleration.
Are these equations used in everyday life?
Yes, they are applied in fields like transportation, sports, and engineering.
What happens if acceleration is zero?
The object moves at a constant velocity, and the equations simplify accordingly.