Do you know what is work done in physics? It is a fundamental concept that sets the foundation for concepts like energy and power.

Introduction

It is very interesting to know that when a person carries a pail from one place to the other horizontally, the work done by the person on the pail is zero. Similarly, when a person pushes against a stationary wall, according to physics, no work is done either.

The question is, why does it happen?

Let us assume in both cases a constant force is acting. However, for the former, the force exerted by the person is perpendicular to the horizontal displacement, meaning $\theta = 90^\circ$ , and for the latter, the wall does not move, meaning the displacement is zero.

Now, the question is, how does it happen?

To understand the underlying reason, we need to look at the definition of work from the perspective of physics. In physics, the concept of work is foundational to understanding how forces interact with motion.

What is Work in Physics?

In physics, the work is defined as,

“the product of force and the displacement travelled in the direction of the force on an object.”

“the dot product of force and displacement.”

Key Characteristics of Work

Representation

Work done is represented by the symbol $W$ .

Unit

The SI unit of work is the joule ( $J$ ), also called $Nm$ or $kg m^{2}s^{-2}$ .

Type of Quantity

Work is a derived physical quantity because it depends on other physical quantities such as force and displacement.

Nature of Quantity

Work is a scalar quantity, meaning it has magnitude but no direction.

Mathematical Formulation

Consider a scenario where a child drags a cart using a rope with a constant force, applied at an angle to the direction of motion.

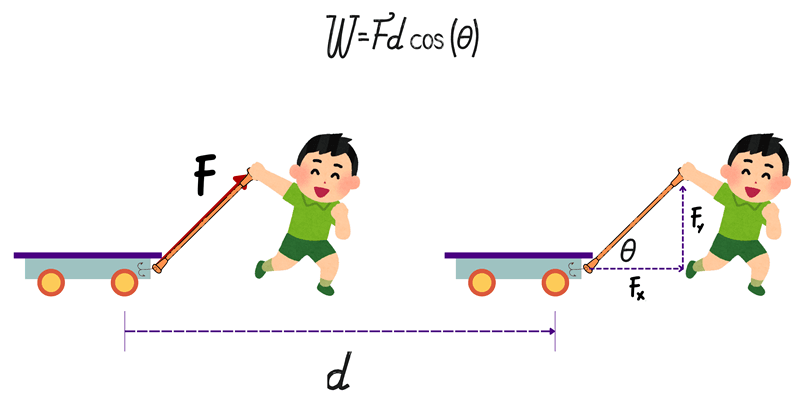
Here,

$F$ = applied force (inclined)
$d$ = distance covered due to force
$\theta$ = angle between $\vec{F} \amp \vec{d}$

Since the force is inclined, we shall resolve it into its perpendicular components. As shown in the figure,

$F_x$ = Horizontal Component of Force

$F_y$ = Vertical Component of Force

Also, it is clear from the figure,

distance covered along $F_x = d$

distance covered along $F_y = 0$

According to the definition of work,

$\text{Work Done} = \text{Effective Force} \times \text{Distance in the Direction of Force}$

Along x-axis

$W = F_x \times d$

According to trigonometry,

$F_x = F \cos\left(\theta\right)$

Hence,

$W = F \cos\left(\theta\right) \times d$

Along y-axis

$W = F_y \times 0$

$W = 0$

Total Work Done

Combining the contributions from both components:

$W = W_x + W_y$

$W = F \cos(\theta) \cdot d + 0$

$W = F \cdot d \cdot \cos \theta$

This can also be expressed in vector form.

$W = \vec{F} \cdot \vec{d}$

Here,

$W = \text{total work done}$

Work Done at Different Angles

Depending upon the angle, the magnitude of the work can either be positive, zero, or negative.

1. Positive Work

Work is positive, when the $\vec{F }$ and $\vec{d}$ are like-parallel, (or lie between $0^\circ \leq \theta < 90^\circ$ ).

Example

Pulling a box with a rope on a flat frictionless surface.

$W = F \cdot d \cdot \cos 0^\circ$

$W = F \cdot d \quad \text{(max)}$

2. Zero Work

Work is zero when the $\vec{F }$ and $\vec{d}$ are perpendicular (i.e., $\theta = 90^\circ$ ).

Example

Carrying a bag in the hand while moving horizontally.

$W = F \cdot d \cdot \cos 90^\circ$

$W = 0$

3. Negative Work

Work is negative when the $\vec{F}$ and $\vec{d}$ are unlike parallel, (or $90^\circ < \theta \leq 180^\circ$ ).

Example

Friction that acts between a course surface and the object opposes its motion.

$W = F \cdot d \cdot \cos 180^\circ$

$W = -F \cdot d \quad \text{(min)}$

Graphical Representation of Work

The work done by a force can also be visualised on a force-displacement graph as shown.

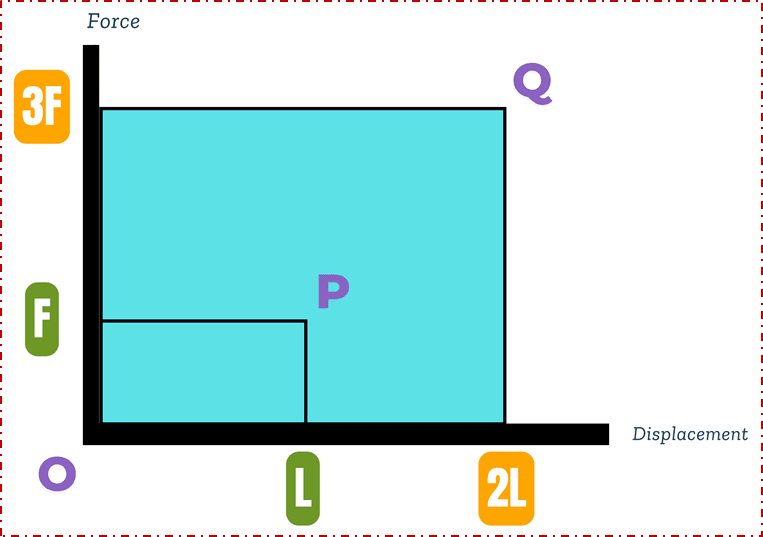
For graph line $\left(1\right)$ , force $F$ acts through a distance $d$ . For graph line $\left(2\right)$ , the force is increased to $3F$ and acts through a further distance of $2L$ . The area under these graph lines gives the total work done.

$\text{Work Done} = \text{Area Under Graph Line}$

$\text{Work Done} = \text{Area of Rectangle}$

$W = \text{length} \times \text{breadth}$

For Graph Line (FP)

$W = L \times F$

For Graph Line (3FQ)

$W = 2L \times 3F$

$W = 6 L F$

Constant Force

For a constant force, the graph is a horizontal line, and the area under the graph line (a rectangle) represents the work done.

Variable Force

For a variable force, the graph is not a straight line. The work done is calculated as the area under the curve, however, by dividing the displacement into small intervals and summing the areas of rectangles or trapezoids.

What is Joule?

One joule is defined as the work done when a force of one newton displaces an object by one meter in the direction of the force.

$1 J = 1 N \cdot 1 m$

Conclusion

Understanding the concept of work provides a foundation for exploring energy, power, and more complex mechanical systems. Whether it is calculating the work done by a machine or analysing forces in everyday life, this principle is the key to bridging the gap between theoretical physics and practical applications.

So, next time when you carry a load and walk for a couple of miles, remember you have done no work (as per the physics definition).

Frequently Asked Questions (FAQs)

What is work done in physics?

Work done is the product of the force applied to an object and the displacement of the object in the direction of the force.

Mathematically,

$W = \vec{F} \cdot \vec{d}$

$W = F \cdot d \cdot \cos\theta$ .

What is the SI unit of work?

The SI unit of work is the joule (J). One joule is the work done when a force of 1 newton displaces an object by 1 meter in the direction of the force.

Why is no work done when carrying an object horizontally?

When carrying an object horizontally, the force applied (upward to counteract gravity) is perpendicular to the displacement (horizontal), so $\theta = 90^\circ$ . As $\cos 90^\circ = 0$ , no work is done.

What are the conditions for work to be done?

A force must be applied.
The object must be displaced.
There must be a component of force along the direction of displacement.

How can work be positive, zero, or negative?

Positive work: Force and displacement are in the same direction $\left(0^\circ \leq \theta < 90^\circ \right)$ .

Zero work: Force is perpendicular to displacement $\left(\theta = 90^\circ\right)$ .

Negative work: Force opposes the displacement $\left(90^\circ < \theta \leq 180^\circ \right)$ .

How is work represented graphically?

On a force-displacement graph, the area under the graph line represents the work done. For constant forces, the area is a rectangle; for variable forces, the area under the curve is calculated by calculus.

What is the difference between constant and variable forces regarding work?

Constant force: Work is calculated as $W = F \cdot d$ .

Variable force: Work is found by integrating the force over displacement or summing small intervals.

What is the practical significance of work in physics?

Understanding work helps in analysing energy transfer, calculating machine efficiency, and solving problems related to power and mechanical systems.

What happens to the work done if the angle between force and displacement increases?

As the angle increases, $\cos\theta$ decreases. The work done reduces and becomes zero at $90^\circ$ . Beyond $90^\circ$ , work becomes negative, indicating opposition to motion.

Ali Abdullah

15 April 2025 at 10:56 PM

This blog post easily breaks down the idea of work in physics into definition, formula, and various situations using understandable examples. It clearly explains how apparently strenuous activities can be zero work from a physics point of view.

admin
18 April 2025 at 12:48 AM
Thank you for your feedback. Explore more.

What is Work Done in Physics by a Constant Force? | 101 A Comprehensive Guide

Table of Contents

Introduction

What is Work in Physics?

Key Characteristics of Work

Representation

Unit

Type of Quantity

Nature of Quantity

Mathematical Formulation

Total Work Done

Work Done at Different Angles

1. Positive Work

2. Zero Work

3. Negative Work

Graphical Representation of Work

Constant Force

Variable Force

What is Joule?

Conclusion

Frequently Asked Questions (FAQs)

What is work done in physics?

What is the SI unit of work?

Why is no work done when carrying an object horizontally?

What are the conditions for work to be done?

How can work be positive, zero, or negative?

How is work represented graphically?

What is the difference between constant and variable forces regarding work?

What is the practical significance of work in physics?

What happens to the work done if the angle between force and displacement increases?

2 thoughts on “What is Work Done in Physics by a Constant Force? | 101 A Comprehensive Guide”

Leave a Comment Cancel Reply