In classical mechanics, the law of conservation of energy derivation and the concept of interconversion of potential energy and kinetic energy form the bedrock of how we analyse physical systems.

Introduction

The law of conservation of energy is also known as the principle of conservation of energy. This principle is essential across physics, engineering, biomechanics, and environmental science. It helps us to model everything from a falling apple to the intricate motion of machines.

By exploring the interconversion of kinetic energy and potential energy, we can better understand the conservation of mechanical energy which is an extremely powerful tool in understanding the motion of objects.

Total Mechanical Energy

Total mechanical energy (M.E.) is the sum of kinetic energy (K.E.) and potential energy (P.E.) in a system.

If there is no external work done (like friction or air resistance), the total mechanical energy remains constant.

Mathematical Formulation

It is given as;

$\text{Total Mechanical Energy} = \text{K.E.} + \text{P.E.} = \text{constant}$

Total Mechanical Energy of a Physical System

Kinetic Energy (K.E.) is the energy due to the motion of an object.

$\text{K.E.} = \frac{1}{2}mv^2$

Here,

$m = \text{mass}$

$v = \text{speed}$

Doubling the speed will quadruple the K.E.

Potential Energy (P.E.) is the energy due to position (usually height in a gravitational field):

$\text{P.E.} = mgh$

Here,

$g = \text{gravitational acceleration }$

$h = \text{height}$

The height $h$ is above a reference level.

Law of Conservation of Energy

The law states that;

“Energy can neither be created nor be destroyed and can only be converted from one form to another.”

“In a closed system, no energy enters or leaves and the total energy remains constant over time.”

Derivation of Law of Conservation of Energy

Mathematical Formulation

Mathematically, it is given as:

$\text{Initial Energy} = \text{Final Energy}$

In the case of mechanical systems:

$\text{Initial K.E.} + \text{Initial P.E.} = \text{Final K.E.} + \text{Final P.E.}$

This relationship forms the basis of energy conservation in classical mechanics.

Derivation of Interconversion of Potential Energy and Kinetic Energy

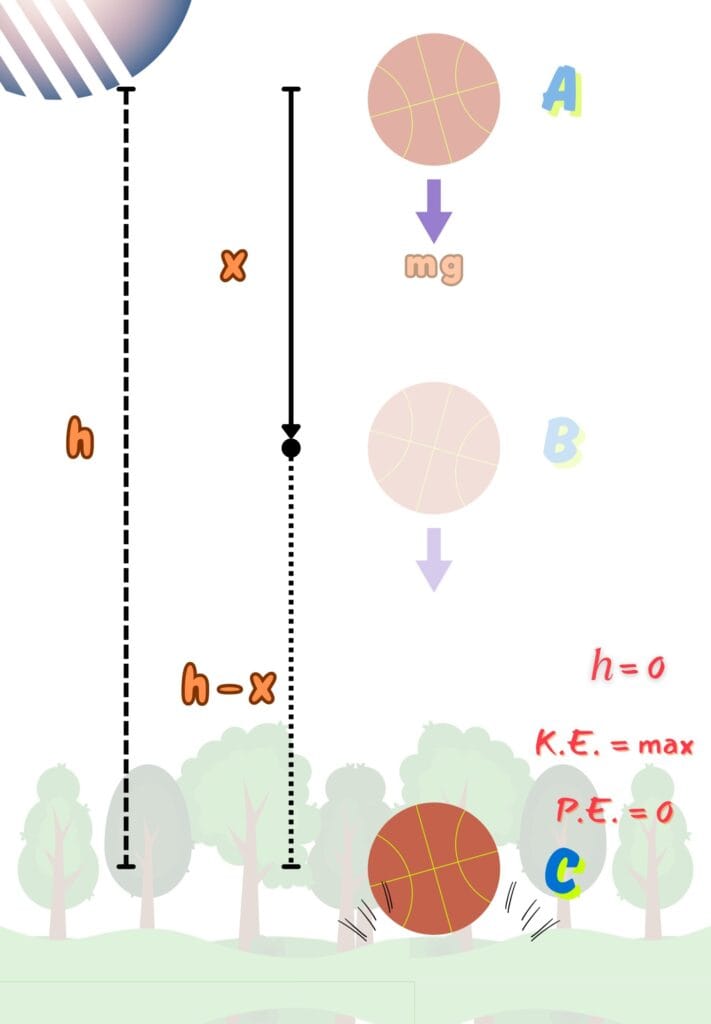
Consider an object is moving under the influence of gravity and its energy shifts between kinetic and potential forms as shown.

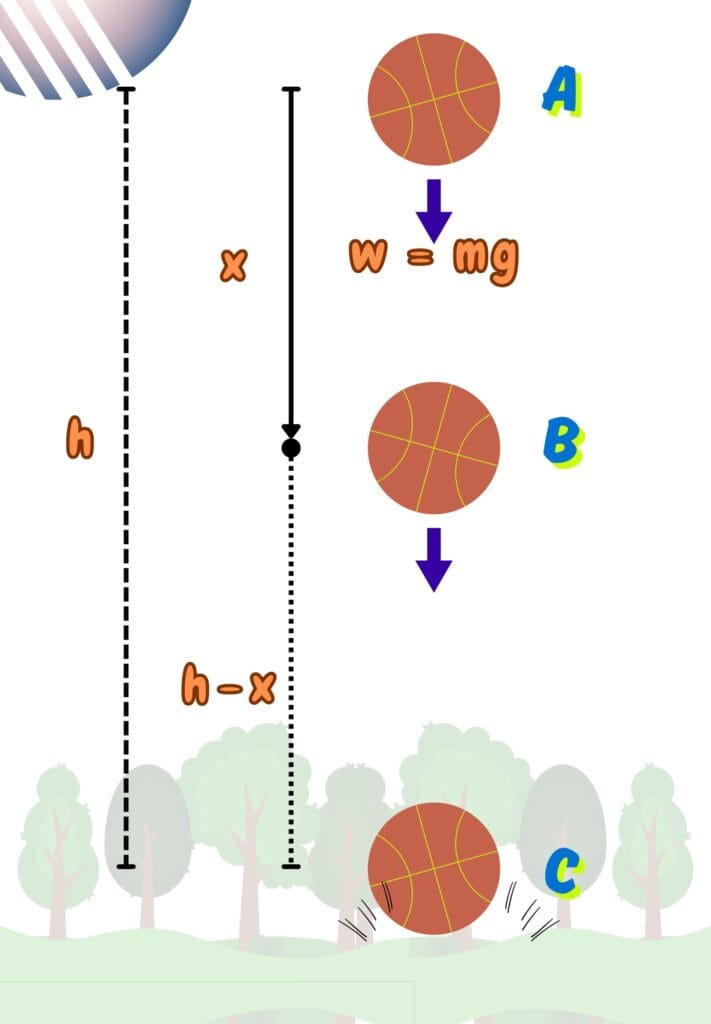
Law of Conservation of Energy Derivation - A Falling Ball

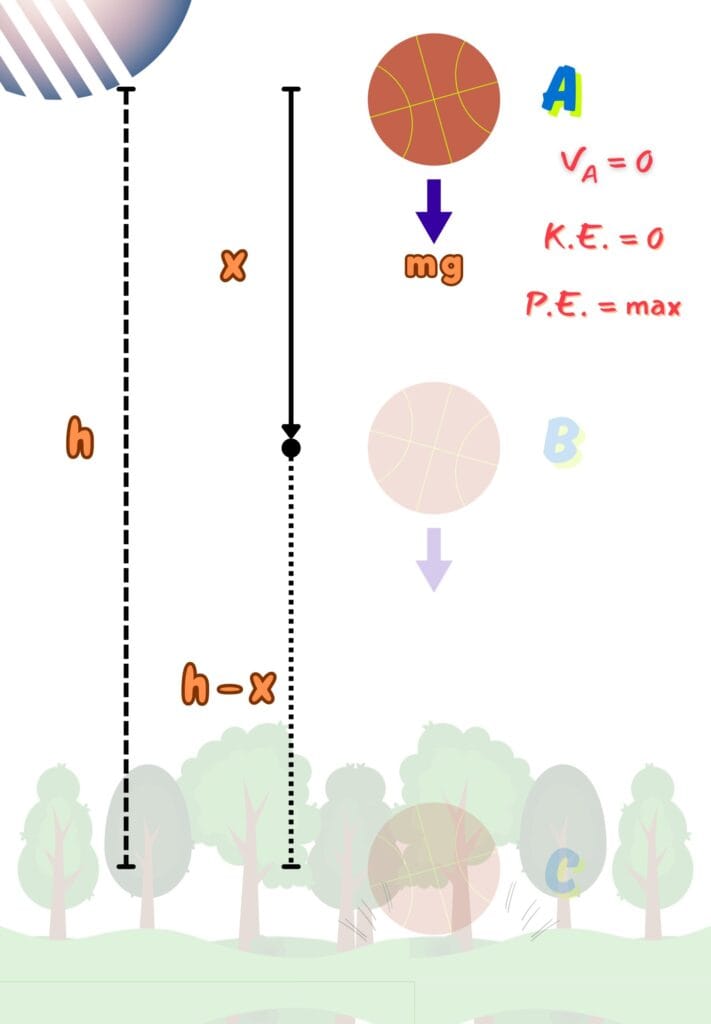
At the top (Position A)

When the object is at the highest place;

Interconversion of Potential Energy into Kinetic Energy - A Falling Ball At the Top

$\text{speed of the object} = v_A = 0$

$\text{height above the ground} = h$

The P.E. at point A,

$\text{P.E.} = mgh$

The K.E. at point A,

$\text{K.E.} = \frac{1}{2}mv_A^2$

$\text{K.E.} = 0$

Hence,

$\text{Total Mechanical Energy} = \text{K.E.} + \text{P.E.}$

$\text{M.E.} = 0 + mgh$

$\text{M.E.} = mgh$

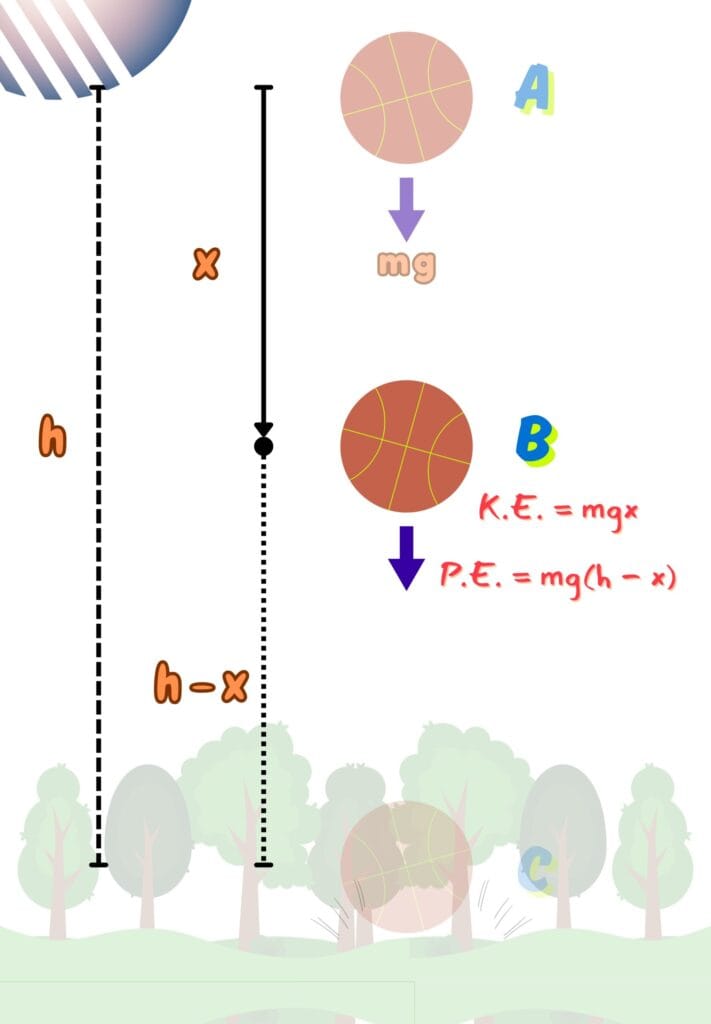
At the Midway (Position B)

After falling through a distance $x$ ;

Interconversion of Potential Energy into Kinetic Energy - A Falling Ball At the Midway

$\text{speed of the object} = v_B$

$\text{distance from A to B} = x$

$\text{height above the ground} = h - x$

The P.E. at point B,

$\text{PE} = mg \left( h - x \right)$

$\text{PE} = mgh - mgx \right)$

The K.E. at point B,

$\text{KE} = \frac{1}{2}mv^2$

For a falling body, the 3^rd equation of motion is given as,

$2gx = v_B^2 - v_A^2$

Since $v_A = 0$ ,

$v_B^2 = 2gx$

The K.E. at point B changes to,

$\text{K.E.} = \frac{1}{2}m \left(2gx\right)$

$\text{K.E.} = mgx$

Hence,

$\text{Total Mechanical Energy} = \text{K.E.} + \text{P.E.}$

$\text{M.E.} = mgx + mgh - mgx$

$\text{M.E.} = mgh$

At the Bottom (Position C)

When the object is just about to hit the ground;

Interconversion of Potential Energy into Kinetic Energy - A Falling Ball At the Bottom

$\text{speed of the object} = v_C \quad \to \text{max}$

$\text{height above the ground} = h = 0$

The P.E. at point C,

$\text{P.E.} = mgh$

$\text{P.E.} = 0$

The K.E. at point C,

$\text{K.E.} = \frac{1}{2}mv_C^2$

For a falling body,

$2gh = v_C^2 - v_A^2$

Since $v_A = 0$ ,

$v_C^2 = 2gh$

The K.E. at point C transforms to,

$\text{K.E.} = \frac{1}{2}m \left(2gx\right)$

$\text{K.E.} = mgh$

Hence,

$\text{Total Mechanical Energy} = \text{K.E.} + \text{P.E.}$

$\text{M.E.} = mgh + 0$

$\text{M.E.} = mgh$

Interpretation of Interconversion of Potential Energy and Kinetic Energy

This interconversion demonstrates,

$\text{M.E. at A} = \text{M.E. at B} = \text{M.E. at C}$

$\text{Loss in P.E.} = \text{Gain in K.E.}$

In other words,

$\text{As } h \uparrow, \quad \text{K.E.} \downarrow \quad \text{and} \quad \text{P.E.} \uparrow$
$\text{As } h \downarrow, \quad \text{K.E.} \uparrow \quad \text{and} \quad \text{P.E.} \downarrow$

What about Friction?

In the real world, due to non-conservative forces like friction or air resistance, some mechanical energy is lost as thermal energy.

In this case, the energy balance is given as;

$\text{Loss in P.E.} = \text{Gain in K.E.} + \text{Work done against friction } f$

$\text{Loss in P.E.} = \text{Gain in K.E.} + f h$

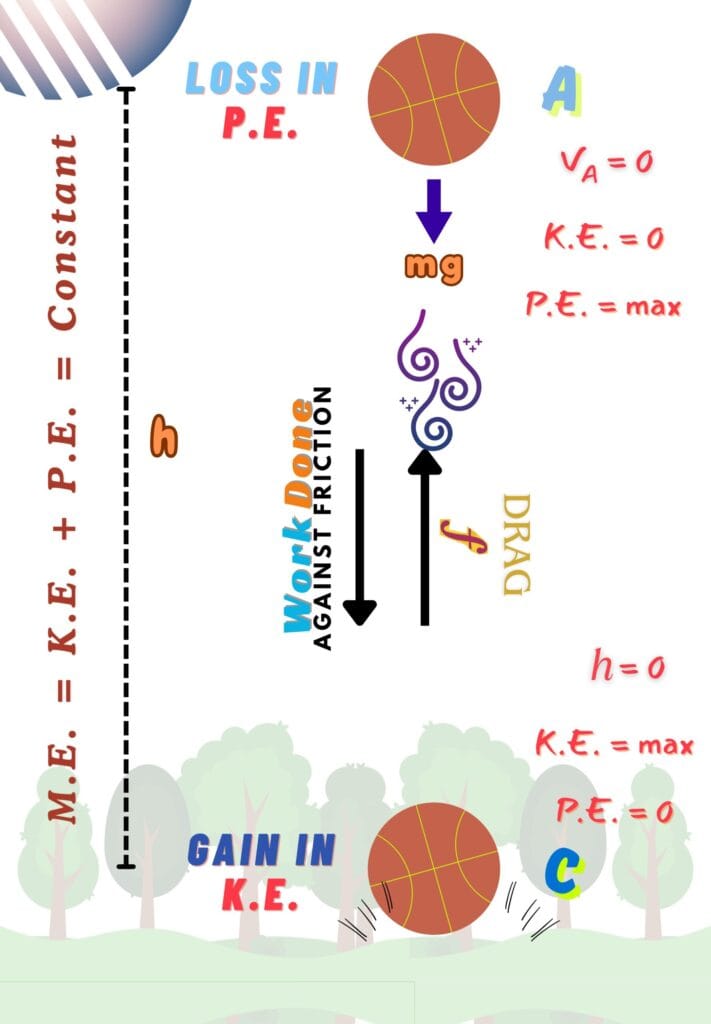
Non-Conservative Force and Law of Conservation of Energy

Interpretation of Law of Conservation of Energy Derivation

This relationship validates 2 important points;

1. Total mechanical energy is not conserved in the presence of non-conservative forces

2. M.E. is always conserved–neither created nor destroyed just transformed into heat, sound, etc.

Energy Transformations in the Real World

Everyday life is full of energy conversions. For instance;

A roller coaster transforms P.E. into K.E. and back again as it moves.
An electric motor converts electrical potential energy into mechanical motion.
In our bodies, chemical potential energy from food turns into thermal and kinetic energy.

Examples of Energy Transformations in the Real World

Eventually, due to inefficiencies and friction, much of this energy transforms into unusable heat. This contributes to the overall entropy of the system. That is why finding sustainable and efficient energy sources is so vital.

Conclusion

Kinetic and potential energy and the principle of conservation of mechanical energy are more than just textbook ideas. They are crucial to analysing and predicting the behaviour of physical systems.

Whether we are modelling a clock pendulum, launching a spacecraft, or designing a bridge, these fundamental concepts provide clarity, insight, and a strong foundation for both theoretical and applied physics.

Frequently Asked Questions (FAQs)

What does the energy possessed by a body by virtue of its position call?

This energy is called potential energy (P.E.).

The magnitude of the momentum of an object is doubled. The kinetic energy of the object will be?

As we know,

$\text{K.E.} = \frac{1}{2}mv^2$

From the definition of momentum;

$p = mv$

$v = \frac{p}{m}$

$\text{K.E.} = \frac{1}{2}m \left(\frac{p}{m}\right)^2$

$\text{K.E.} = \frac{p^2}{2m}$

According to the condition;

$p' = 2p$

$\text{K.E.}' = \frac{{p'}^2}{2m}$

$\latex{K.E.}' = \frac{(2p)^2}{2m} = \frac{4 p^2}{2m} = 4 \times \frac{p^2}{2m} = 4 \text{K.E.}$

So, kinetic energy becomes quadrupled.

What is the potential energy of a body of mass $m$ when it is raised through a height $h$ ?

In such a case,

$P.E. = mgh$

Here,

$g = \text{acceleration due to gravity}$

Find an expression for the kinetic energy of a moving body.

The kinetic energy of the body can be expressed as,

$\text{Kinetic Energy of the Body} = \text{Work Done by the Body due to Motion}$

$\text{K.E} = \text{W}$

$\text{K.E} = F S$

$\text{K.E} = \frac{\Delta p}{t} S$

$\text{K.E} = \left(m v_f - m v_i\right) \frac{v_f + v_i}{2}$

$\text{K.E} = \left(m \cdot v - m \cdot 0\right) \frac{v + 0}{2}$

$\text{K.E} = \frac{1}{2}mv^2$

Can kinetic energy of a body be negative?

No!

Reason

As we know,

$\text{K.E} = \frac{1}{2}mv^2$

Since,

$m \to \text{positive}$
$v^2 \to \text{positive}$

Hence,

$\text{K.E.} \to \text{positive}$

Which one has greater kinetic energy; an object travelling with velocity $v$ or an object twice as heavy travelling with velocity $\frac{1}{2}v$ ?

Let usLet us consider,

For object A

$\text{K.E.}_1 = \frac{1}{2}mv^2$

For object B

$\text{Mass} = 2m, \quad \text{Velocity} = \frac{1}{2}v$

$\text{K.E.}_2 = \frac{1}{2}(2m)\left(\frac{1}{2}v\right)^2$

$\text{K.E.}_2 = m \cdot \frac{v^2}{4}$

$\text{K.E.}_2 = \frac{1}{4}mv^2$

So, object A has greater kinetic energy. consider,

Comment on the statement: “An object has one joule of potential energy.”

This means the object can do one joule of work due to its position.

Let,

$\text{height above the ground = 1 m}$
$\text{mass of the object = 0.102 kg}$

Since,

$\text{P.E.} = mgh = 0.102 \times 9.8 \times 1 \approx 1 J$

While driving on a motorway, the tyres of a vehicle often burst. What may be its cause?

Due to high speed, friction between tyres and the road increases, causing the temperature and pressure inside the tyre to rise. When a certain limit of temperature and pressure exceeds, the tyre bursts.

A man rowing a boat upstream is at rest with respect to the shore. Is he doing work?

Yes, he is doing work against the current.

Reason

Work is done when a force causes an object to move a certain distance. Even though, in this case, there is no displacement relative to the shore. The man is still applying force on the oars, and the oars are moving through the water.

Law of Conservation of Energy Derivation | Interconversion of Potential Energy and Kinetic Energy | 2 Mechanical Energies Simplified

Table of Contents

Introduction

Total Mechanical Energy

Mathematical Formulation

Law of Conservation of Energy

Mathematical Formulation

Derivation of Interconversion of Potential Energy and Kinetic Energy

At the top (Position A)

At the Midway (Position B)

At the Bottom (Position C)

Interpretation of Interconversion of Potential Energy and Kinetic Energy

What about Friction?

Interpretation of Law of Conservation of Energy Derivation

Energy Transformations in the Real World

Conclusion

Frequently Asked Questions (FAQs)

What does the energy possessed by a body by virtue of its position call?

The magnitude of the momentum of an object is doubled. The kinetic energy of the object will be?

What is the potential energy of a body of mass $m$ when it is raised through a height $h$ ?

Find an expression for the kinetic energy of a moving body.

Can kinetic energy of a body be negative?

Which one has greater kinetic energy; an object travelling with velocity $v$ or an object twice as heavy travelling with velocity $\frac{1}{2}v$ ?

Comment on the statement: “An object has one joule of potential energy.”

While driving on a motorway, the tyres of a vehicle often burst. What may be its cause?

A man rowing a boat upstream is at rest with respect to the shore. Is he doing work?

Leave a Comment Cancel Reply