Here, we shall learn the answer to “What is pressure in physics?” and “How pressure is measured in different states of matter i.e. solid, liquid, and gas?” Besides, we shall also learn about types of pressure, real-life applications, and the science behind it.

Introduction

From the way air keeps airplanes aloft to how submarines dive, the understanding of pressure has contributed to our lives greatly. Even the way deep-sea creatures survive intense ocean depths and the way weather patterns change are examples that require an understanding of pressure.

It is a fundamental concept in physics. It enables us to understand how forces are distributed over a surface. It plays a central role in various natural and technological phenomena.

What Is Pressure?

In physics, pressure is defined as,

“the force applied per unit area.”

Key Characteristics of Pressure

Representation

It is represented by the symbol $P$ .

Unit

Its SI unit is the Pascal ( $Pa$ ), also called $N m^{-2}$ .

Note

The SI unit of pressure is named after Blaise Pascal, a French mathematician, physicist, and inventor. There are some other units of pressure as well which are used in engineering and earth sciences.

Bar $\left(1 \text{ bar} = 100,000 \text{ Pa}\right)$
Atmosphere $\left(1 \text{ atm} = 101,325 \text{ Pa}\right)$
Torr $\left(1 \text{ atm} = 760 \text{ torr}\right)$
Pounds per square inch $\left(1 \text{ psi} = 6 894.76 \text{ Pa}\right)$

Type of Quantity

It is a derived physical quantity that depends on the exerted force and surface area of the object.

Nature of Quantity

It is a scalar quantity (a quantity that only requires magnitude).

Mathematical Formulation

Mathematically, it is expressed as;

$P = \frac{F}{A}$

Here,

$P = \text{pressure}$

$F = \text{force}$

$A = \text{area}$

Daily Life Examples of Pressure

Sports Shoes vs. High Heels

Sports shoes have a larger sole area, so your body weight is spread over a larger surface, resulting in less pressure on the ground.

High heels have a small contact area, so the same weight produces much higher pressure, which can even dent wooden floors or sink into soft ground.

Sports Shoes vs. High Heels and Pressure

Mathematically, it can be seen as follows:

$P_1 = \frac{F_1}{A_1} \quad \to \text{for sports shoes}$

$P_2 = \frac{F_2}{A_2} \quad \to \text{for high heels}$

If a woman wears either of these, her weight (force) remains the same i.e.

$F_1 = F_2$

Since,

$A_1 > A_2$

Hence,

$P_1 < P_2$

This shows high heels cause more discomfort (pressure) than sports shoes.

Chopper Blade vs. Sledgehammer

The chopper blade possesses a sharp edge which means it has a minuscule area. When force is applied, the pressure is high, making it easier to cut through vegetables or meat.

On the other hand, a sledgehammer has a broader head. It delivers the force over a slightly larger area to ensure that the nail gets in by impact force and does not do the cutting.

Chopper Blade vs. Sledgehammer and Pressure

Walking on Smooth vs. Rough Roads

On smooth surfaces, pressure is distributed evenly, so it feels comfortable to walk even when we are bare feet.

Contrarily, on rough surfaces, pebbles create high pressure at specific points due to their smaller area, causing discomfort or pain.

Walking on Smooth vs. Rough Roads and Pressure

Different Animal Feet

Heavy animals (like an elephant) have broad, padded feet. This distributes their weight over a large area, resulting in low pressure. The larger feet help them not to sink into the sand.

Light animals (like a deer) have narrow and hard hooves. This concentrates the weight in a smaller area, resulting in high pressure. The small feet dig into the ground, giving them better traction.

Thumb Pin (Drawing Pin)

When we press a thumb pin, the force we apply is spread over a large head. Due to this, the force is concentrated at the tiny point of the pin. This creates very high pressure at the tip and allows the pin to pierce paper or soft boards easily.

Types of Pressure

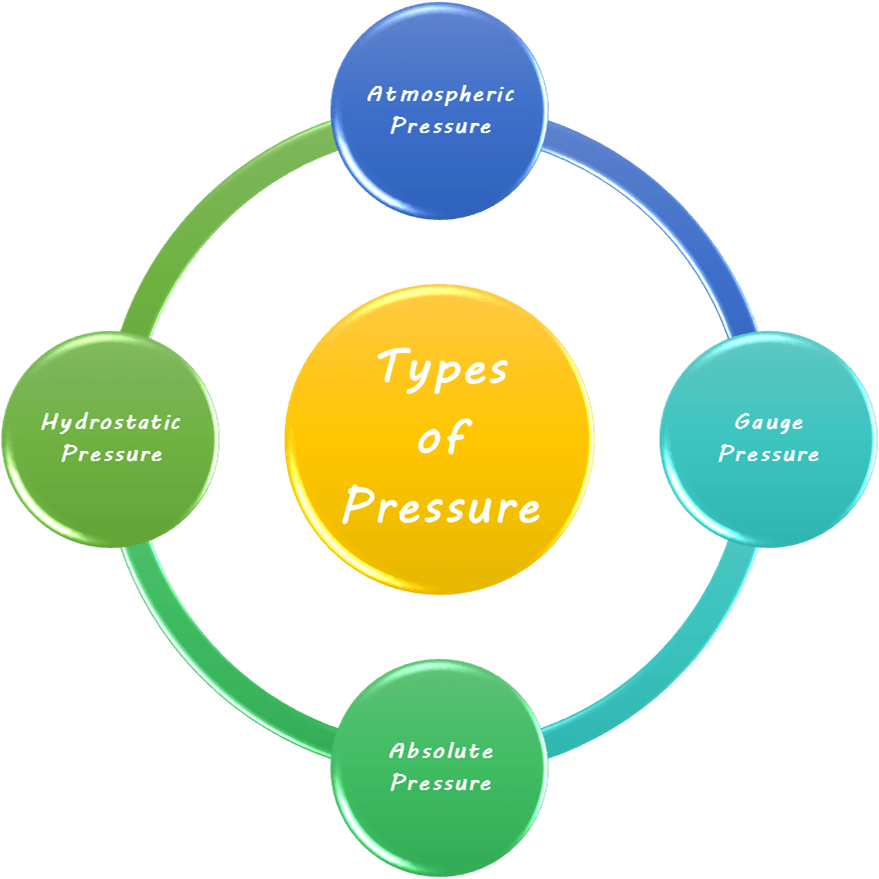
Atmospheric Pressure

This is the pressure exerted by the weight of the atmosphere of Earth at sea level. It is about 101.3 kPa or 1 atm and decreases with altitude.

Gauge Pressure

It is the pressure measured by a pressure gauge relative to atmospheric pressure. It is often seen while inflating car tyres or in pressure cookers.

Note that gauge pressure can be negative. It is the pressure below the atmospheric pressure and happens in situations involving vacuum gauges.

Absolute Pressure

This is the total pressure measured relative to a perfect vacuum. It is related to atmospheric pressure and gauge pressure as follows;

$\text{Absolute Pressure} = \text{Gauge Pressure} + \text{Atmospheric Pressure}$

Hydrostatic Pressure

The pressure exerted by a fluid (like water) at equilibrium due to the force of gravity. It increases with depth in a fluid and is given by,

$P = \rho g h$

Here,

$\rho = \text{fluid density}$
$g = \text{acceleration due to gravity}$
$h = \text{height (or depth) of fluid}$

Pressure in Solids, Liquids, and Gases

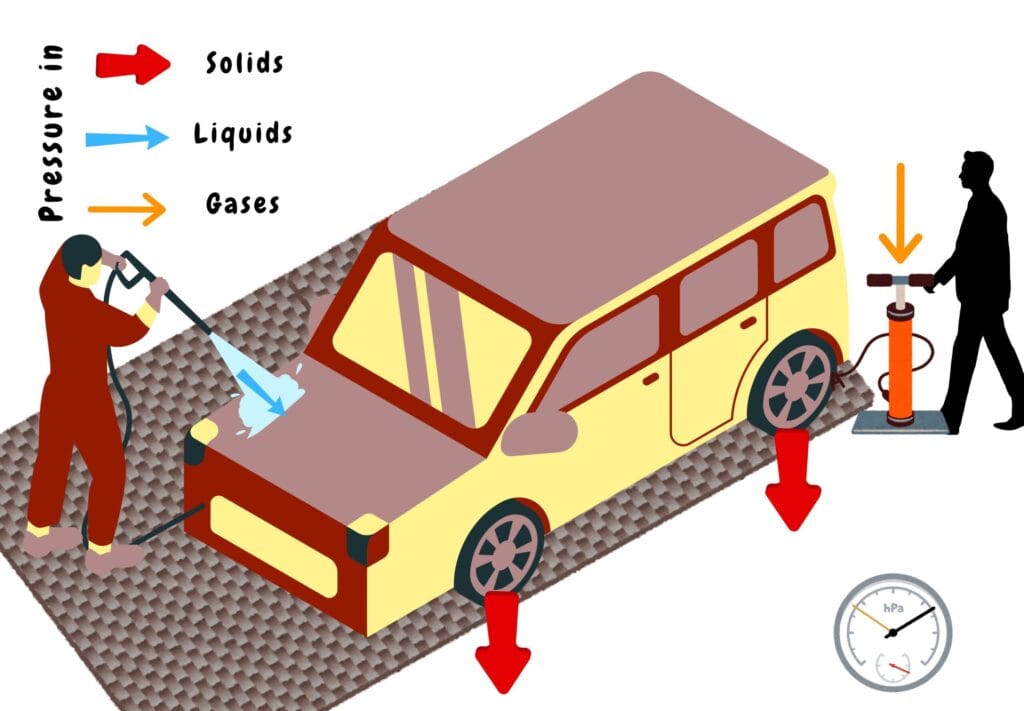
In Solids

Pressure in solids is usually seen as a contact force distributed over an area. This pressure acts normally on the surface and does not spread in all directions, unlike fluids.

Derivation of $P = \frac{F}{A}$

Let an object apply the force $'F'$ uniformly over a surface area $'A'$ .

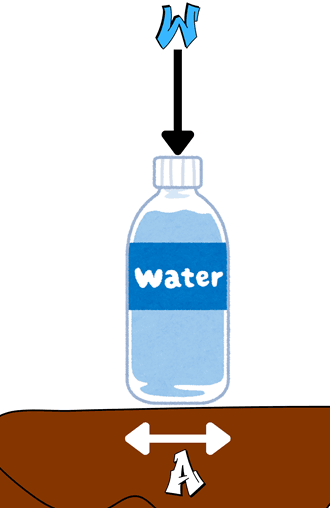
According to the definition;

$P = \lim_{\Delta A \to 0} \frac{\Delta F}{\Delta A}$

$P = \frac{F}{A}$

This equation proves a smaller area and higher force result in higher pressure—explaining why sharp objects cut better.

In Liquids

Pressure in liquids is usually seen as a gravitational force exerted by a fluid at its equilibrium position. It is transmitted in all directions of the surface in contact.

Derivation of $P = \rho g h$

Consider a liquid column of height $h$ and cross-sectional area $A$ .

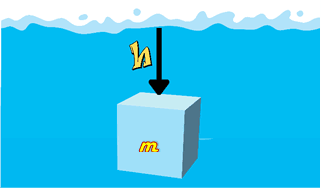
According to the definition;

$P = \frac{F}{A}$

According to the definition of force,

$F = m \times g$

Since,

$m = \rho V$

Here,

$\rho = \text{density}$

$V = \text{volume}$

$V = A h$

Replacing all the values, we get;

$m = \rho A h$

$F = \rho A h \times g$

Hence, pressure is given as;

$P = \frac{\rho A h g}{A}$

$P = \rho g h$

The equation shows the rise in pressure is associated with the depth of the column of fluid—resulting in a thicker bottom of the dam.

In Gases

Pressure in gases is seen as the collisions of molecules against the walls of their container. This behaviour is explained by the kinetic theory of gases.

Derivation of $P = \frac{1}{3} \rho \bar{v}^2$

The kinetic theory of gases explains the behaviour of pressure in gases. Here, its derivation will be not included for brevity.

$P = \frac{1}{3} \rho \bar{v}^2$

Here,

$\rho = \text{gas density}$

$\bar{v}^2 = \text{mean square speed of gas molecules}$

The equation shows that pressure increases with both the density of gas and the average kinetic energy of molecules, which is related to temperature.

Applications of Pressure in Real Life

Some of the real-life applications of pressure are;

Barometers and Altimeters
Hydraulic Systems
Pressure Cookers
Scuba Diving
Aviation

Fun Facts about Pressure

Vacuum chambers can simulate outer space by removing nearly all atmospheric pressure.
The deepest point in the ocean, the Mariana Trench, experiences over 1,000 times the atmospheric pressure at sea level.

Conclusion

Pressure is more than just a scientific formula or a number on a tyre gauge or a weather forecast. It is a key player in understanding how forces manifest in the physical world.

Whether we study physics or are just curious about how things work, the concept of pressure opens up a whole new dimension of knowledge about the universe around us. It explains natural events, engineering marvels, and everyday tools.

From understanding why our ears pop in an airplane or a mountain area to how a hydraulic jack lifts a car, pressure helps to make sense of all these physical world phenomena.

Frequently Asked Questions (FAQs)

What is pressure in Physics?

Pressure is defined as the force exerted per unit area.

Mathematically,

$\text{Pressure} = \frac{\text{Force}}{\text{Area}}$

$P = \frac{F}{A}$

In the SI system, it is measured in Pascal (Pa).

Distinguish between force and pressure.

Force is a push or pull acting on an object (measured in Newtons).
Pressure is the effect of force distributed over an area.

In layman’s terms, force is an agency that can change the state of motion or shape of a body and pressure is the effect of that force over an area which can leave a mark if force is concentrated on a small area.

Why do heavy animals like elephants have larger foot areas, and fast-running animals like deer have smaller ones?

Elephants have larger feet to distribute their weight over a larger area, reducing pressure and avoiding sinking into the ground.

Deer have smaller feet to create more pressure, providing better grip and speed.

Why is it painful to walk barefoot on pebbles?

Pebbles have a small surface area, so the same body weight creates more pressure on the foot, causing pain.

How does water pressure 1 meter below the surface of a swimming pool compare to that of a deep lake?

In a fluid, pressure depends on depth, density, and gravity and not on total volume. So, at 1 meter depth, the water pressure is the same in both the swimming pool and the lake.

On what factors does the pressure of a liquid in a container depend? How is it determined?

Pressure depends on:

Density of the liquid $\left(\rho\right)$
Acceleration due to gravity $\left(g\right)$
Depth from the surface $\left(h\right)$

It is calculated as follows;

$P = \rho g h$

Why does pressure drop as we go up a mountain and increase as we go down into the ocean?

On a mountain, air pressure decreases with altitude due to a thinner atmosphere, while in an ocean, water pressure increases with depth because of the weight of the water above.

It is easy to remove air from a balloon but difficult from a glass bottle. Why?

A balloon is flexible, so squeezing it pushes air out easily. On the other hand, a glass bottle is rigid, so we cannot apply pressure directly to expel air.

Table of Contents

Introduction

What Is Pressure?

Key Characteristics of Pressure

Representation

Unit

Note

Type of Quantity

Nature of Quantity

Mathematical Formulation

Daily Life Examples of Pressure

Sports Shoes vs. High Heels

Chopper Blade vs. Sledgehammer

Walking on Smooth vs. Rough Roads

Different Animal Feet

Thumb Pin (Drawing Pin)

Types of Pressure

Atmospheric Pressure

Gauge Pressure

Absolute Pressure

Hydrostatic Pressure

Pressure in Solids, Liquids, and Gases

In Solids

In Liquids

In Gases

Applications of Pressure in Real Life

Fun Facts about Pressure

Conclusion

Frequently Asked Questions (FAQs)

What is pressure in Physics?

Distinguish between force and pressure.

Why do heavy animals like elephants have larger foot areas, and fast-running animals like deer have smaller ones?

Why is it painful to walk barefoot on pebbles?

How does water pressure 1 meter below the surface of a swimming pool compare to that of a deep lake?

On what factors does the pressure of a liquid in a container depend? How is it determined?

Why does pressure drop as we go up a mountain and increase as we go down into the ocean?

It is easy to remove air from a balloon but difficult from a glass bottle. Why?

Leave a Comment Cancel Reply