“What is a number system?” It is like a map that shows how computers think, store, and solve problems using numbers.
Table of Contents
Introduction
Number systems are not just for computer scientists or engineers. If you have ever used a phone, coded a website, or just wondered how tech works — this is for you.
Understanding number systems helps you:
- Make sense of how devices work.
- Read and debug code.
- Speak the native language of machines.
What Is a Number System?
A number system can be defined as:
“A way to represent, store, and process data in a computing system.”
Why Computers Speak in Numbers? A Recap
Previously, you discovered how computers read letters through binary patterns via the ASCII codebook. That understanding answered the following questions:
- How does a computer read?
- Why does it speak only in numbers?
- Why not use actual letters, words, or pictures?
You also witnessed that a computer system only understands electric signals:
- 1 = High voltage (ON)
- 0 = Low voltage (OFF)
The ON/OFF signals are called binary digits or bits.
4 Types of Number Systems
There are 4 main types of number systems in a computing system. Each system uses a different set of symbols (called digits). These number systems include:
| Name | Base | Range (Symbols) | Example | Application |
| Decimal | 10 | 0 – 9 | 192 | Used by humans |
| Binary | 2 | 0, 1 | 11000000 | Used by computers |
| Octal | 8 | 0 – 7 | 011 000 000 OR 600 | Used in Unix permissions, early computers PDP-8 |
| Hexadecimal | 16 | 0 – 9 and A – F | 1100 0000 OR C0 | Used in memory, colour codes, debugging |
Why Do We Need Octal and Hexadecimal?
This is where it gets interesting.
Binary is great for machines but hard for humans to read. For instance:
(10010111001011011101010101010101)2 → Binary
OR
0b10010111001011011101010101010101 → Binary
This notation is too long and confusing. To resolve the problem, octal and hexadecimal number systems are used. For these number systems (Octal and Hex), we need to use the following tables.
- Conversion Table of Octal and Binary (3 bits per digit)
| Octal | Binary |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
(22713352525)8 → Octal
OR
0o22713352525 → Octal
- Conversion Table of Hexadecimal and Binary (4 bits per digit)
| Hexadecimal (Hex) | Binary Digits (Bits) |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
(972D7555)16 → Hex
OR
0x972D7555 → Hex
These versions (Octal and Hex) are much cleaner and easier to understand. It is because:
- They are shortcuts that represent binary in a human-friendly way.
- They make debugging, memory addresses, and colours easier to read.
Octal and Hex are compact and readable substitutes of the binary world.
Conversion of Number Systems | Practice Worksheet
Similar to the conversion of ‘Octal’ and ‘Hex’ into binary, decimal numbers can also be converted into binary. Besides, all number systems can be converted into one another. For instance (see the figure below):
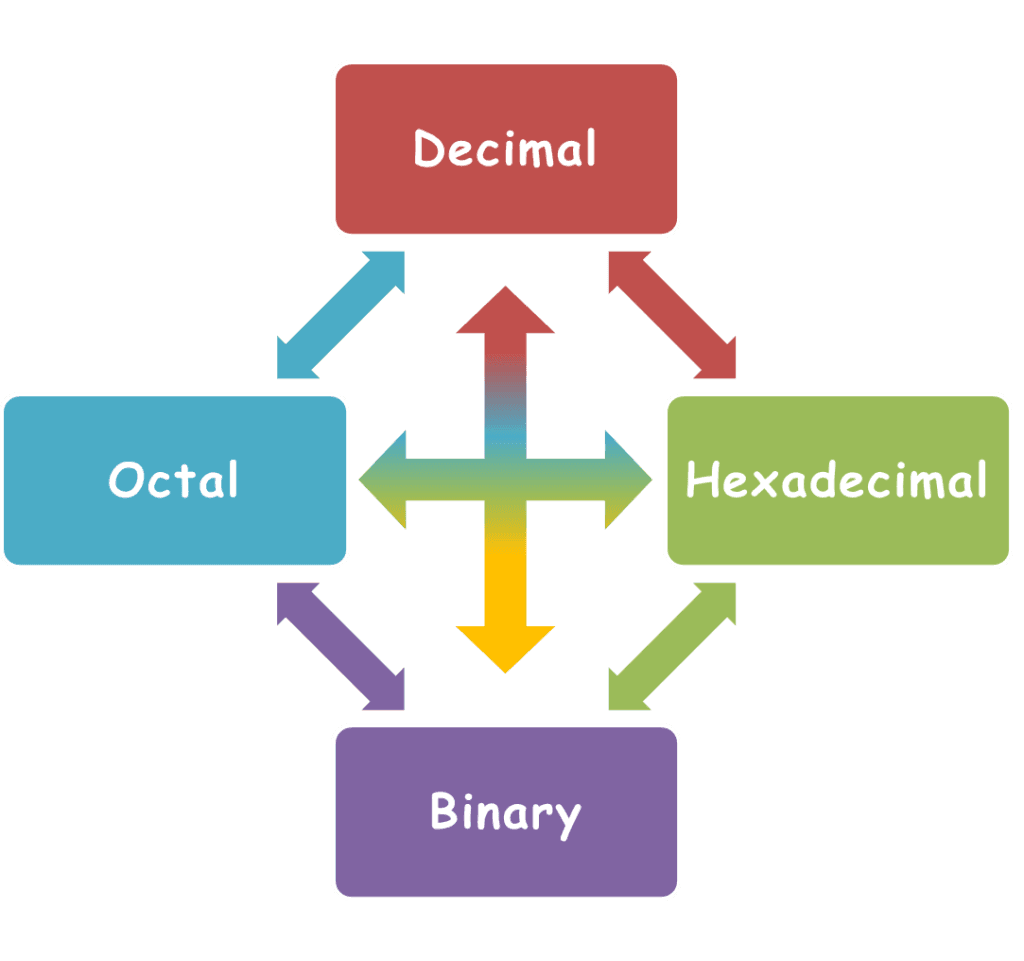
Check out the worksheet given here as a PDF to practice and master the conversion of these number systems.
Conclusion
Understanding the number systems – decimal, binary, octal, and hexadecimal – is not just technical trivia. It gives you:
- Clarity when reading code
- Confidence when debugging
- Power to speak the language beneath the screen
Just like the ASCII code book, you do not need to memorise octal or hexadecimal tables. You just need to understand why they exist and how to utilise them. Because once you do, you are no longer guessing how your computer works — you are reading its mind.
Frequently Asked Questions (FAQs)
What Is a Number System?
A number system is a way to represent, store, and process numbers (data) in a computing system. It defines how values are symbolized using digits and how those digits work together.
Write 4 Types of Number Systems in Computing.
- Decimal (Base 10): Uses digits 0–9.
- Binary (Base 2): Uses digits 0 and 1.
- Octal (Base 8): Uses digits 0–7.
- Hexadecimal (Base 16): Uses digits 0–9 and letters A–F.
Which of the following numbers is a valid binary number?
(a) 1101102 (b) 11011 (c) 110.11 (d) 1101A
(b) 11011 – Valid binary number (contains only 0 and 1)
(c) 110.11 – Valid binary fractional number
What Are Binary Digits (or Bits)?
Binary digits, also called bits, are the smallest units of data in a computer. They have only two possible states:
- 1 = ON (high voltage)
- 0 = OFF (low voltage)
Bits are how computers represent and process all forms of data.
Write Steps Involved in Converting Decimal to Binary, Octal, and Hexadecimal.
To convert a decimal number into binary, octal, or hexadecimal:
1. Divide the decimal number by 2, 8, or 16 respectively.
2. Record the remainder.
3. Repeat the process using the quotient until it becomes 0.
4. Read the remainder in reverse order to get the final result.
Write Steps Involved in Converting Binary, Octal, and Hexadecimal into Decimal.
To convert binary, octal, or hexadecimal to decimal:
1. Multiply each digit by its base raised to the power of its position (from right to left).
- Binary uses base 2
- Octal uses base 8
- Hexadecimal uses base 16
2. Add all the products together to get the decimal equivalent.
Write Steps Involved in Converting Binary to Octal and Hexadecimal.
Binary to Octal
1. Group binary digits into sets of 3 bits, starting from the right.
2. Convert each group into its octal equivalent using a conversion table.
Binary to Hexadecimal
1. Group binary digits into sets of 4 bits, starting from the right.
2. Convert each group into its hexadecimal equivalent using a conversion table.
Write Steps Involved in Converting Octal and Hexadecimal into Binary.
Octal to Binary
Convert each octal digit into a 3-bit binary number using a conversion table.
Hexadecimal to Binary
Convert each hex digit into a 4-bit binary number using a conversion table.
Write Steps Involved in Converting Octal to Hexadecimal and Vice Versa.
Octal → Hexadecimal
1. Convert each octal digit to binary (3 bits per digit).
2. Group the binary into 4-bit sets and convert them into hex digits.
Hexadecimal → Octal
1. Convert each hex digit to binary (4 bits per digit).
2. Group the binary into 3-bit sets and convert them into octal digits.
