Learn about Malus’s Law and the comprehensive mathematical derivation of Malus Law in the simplest mathematical way.

Introduction

If you are here, that means you have already learnt about fundamentals, such as;

These are the introductory topics about polarization. To explore deeper concepts, including the key laws that govern polarized light, a solid grasp of these fundamentals is essential. One such law, called Malus’s Law, is discussed in this guide.

Malus’s Law

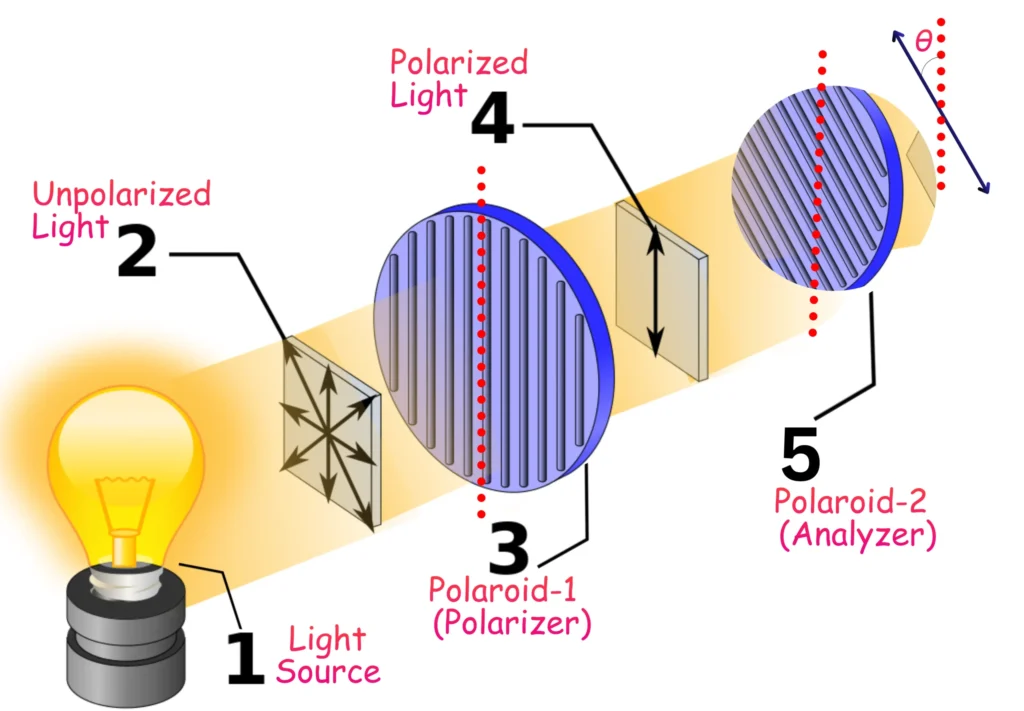
Malus Law describes the intensity of plane-polarized light after passing through an analyzer:

The law is stated as:

“When plane-polarized light passes through an analyzer, the transmitted intensity is proportional to the square of the cosine of the angle between the polarization direction of light and the transmission axis of the analyzer”.

$I = I_0 \cos^2 \theta$

Where:

$I_0 = \text{intensity of light incident on analyzer}$
$\theta = \text{angle between the transmission axes of polarizer and analyzer}$

Mathematical Formulation

The mathematical relationship of Malus’s Law is derived here, for beginners, without advanced concepts of vectors, phasors, or Poynting vectors.

Schematic for Comprehensive Mathematical Derivation of Malus Law

Let!

$\mathbf{E}_0 = \text{electric field amplitude vector of incoming light}$
$\mathbf{A} = \text{vector along analyzer axis}$
$\theta = \text{the angle between } \mathbf{E}_0 \text{ and } \mathbf{A}}$ .

Amplitude Relation

According to the scalar product (dot product):

$\mathbf{E}_0 \cdot \mathbf{A} = |\mathbf{E}_0|\, |\mathbf{A}| \cos \theta \tag{1}$

The goal is to find the component of $\mathbf{E}_0$ along the analyzer axis $\mathbf{A}$ .

Let the magnitude of the incoming light amplitude be:

$A_0 = |\mathbf{E}_0|$

Drawing the projection along the analyzer gives:

$|\mathbf{E}_0| \cos \theta$

From equation (1):

$\mathbf{E}_0 \cdot \mathbf{A} = |\mathbf{E}_0|\, |\mathbf{A}| \cos \theta$

$\Rightarrow \quad |\mathbf{E}_0| \cos \theta = \frac{\mathbf{E}_0 \cdot \mathbf{A}}{|\mathbf{A}|} \tag{2}$

Let $\hat{\mathbf{A}}$ be the unit vector along $\mathbf{A}$ . Then:

If the transmitted amplitude along the analyzer is represented by $A$ , then:

$A = \mathbf{E}_0 \cdot \hat{\mathbf{A}} = |\mathbf{E}_0| \cos \theta$

Since $A_0 = |\mathbf{E}_0|$ , hence:

$\boxed{A = A_0 \cos \theta}$

This equation expresses the amplitude of light transmitted through the analyzer when the angle between the incoming light and the analyzer axis is $\theta$ .

Intensity Relation

The intensity of light can be defined as:

“The energy carried by the wave per unit area per unit time”.

From classical electrodynamic, the energy density of an electromagnetic wave is proportional to the square of the electric field amplitude $E^2$ .

It is written as;

$\text{intensity} \propto \text{amplitude}^2$

Before the Analyzer

Let the incoming plane-polarized light have amplitude $A_0$ . Then its intensity is:

$I_0 \propto A_0^2$

$I_0 = k A_0^2$

$I_0 = \frac{1}{2 c \epsilon_0} A_0^2$

This is the intensity before the analyzer.

Note
In the above relationship;
$k = \text{constant of proportionality} = \frac{1}{2 c \epsilon_0}$
Where,
$c = speed of light$
$\epsilon_0 = \text{permittivity of free space}$

After the Analyzer

Let the outgoing plane-polarized light have amplitude $A$ . Then its intensity is:

To know more about it, see the document below (coming soon). The prerequisites for this document are:
Trigonometry
Calculus (Integral)

$I \propto A^2$

$I = k A^2$

From the scalar product derivation, the transmitted amplitude along the analyzer at angle $\theta$ is:

$A = A_0 \cos \theta$

Hence, the transmitted intensity is:

$I = \frac{1}{2 c \epsilon_0} (A_0 \cos \theta)^2$

$I = \frac{1}{2 c \epsilon_0} A_0^2 \cos^2 \theta$

Since,

$I_0 = \frac{1}{2 c \epsilon_0} A_0^2$

This gives the Malus’s Law:

$\boxed{I = I_0 \cos^2 \theta}$

Extreme Cases

The transmitted amplitude along the analyzer has two possible extremes:

Maximum Transmission $\theta = 0^\circ$
No Transmission $\theta = 90^\circ$

Maximum Transmission

$I = I_0 \cos^2 (0)$

$I = I_0$

No Transmission

$I = I_0 \cos^2 (90)$

$I = 0$

Conclusion

Malus’s Law provides a simple yet powerful mathematical description of plane-polarized light. It tells how polarized light behaves when it encounters an analyzer.

The law shows that the transmitted amplitude of the electric field depends on the cosine of the angle. This angle lies between the polarization direction of the incoming light and the axis of the analyzer.

Moreover, the transmitted intensity—which determines the measurable brightness—depends on the square of this amplitude.

By reducing the physics to simple geometry and the proportionality of intensity with electric-field amplitude squared, you gain an intuitive and mathematically solid view of how polarization-dependent transmission works.

Frequently Asked Questions (FAQs)

State the Malus’s law. Explain the intensity formula.

Malus’s Law states that:

“When plane-polarized light passes through an analyzer, the intensity of transmitted light varies as the square of the cosine of the angle between the transmission axes of the polarizer and the analyzer.”

Mathematically,

$\boxed{I = I_0 \cos^2 \theta}$

Where:

$I_0 = \text{intensity of light incident on the analyser}$
$I = \text{intensity of transmitted light}$
$\theta = \text{angle between the transmission axes of the polarizer and analyser}$

The formula shows that the transmitted intensity depends on the square of the cosineangle. This means the analyzer only transmits the component of the electric field aligned with its transmission axis.

What does happen to the intensity of light when it passes through a polarizer?

When unpolarized light passes through a polarizer, it becomes plane-polarized, and its intensity decreases.

The reason is that out of two perpendicular components, the polarizer only allows vibrations of one component of the electric field to pass through in one direction.

The average transmitted intensity after the polarizer is half the incident intensity:

$I = \dfrac{I_0}{2}$

Write the effect of increasing the angle between the light wave and the analyzer on the intensity of light.

According to Malus’s Law:

$I = I_0 \cos^2 \theta$

As the angle $\theta$ increases, the value of $\cos^2 \theta$ decreases.
Therefore, the transmitted intensity decreases.
When $\theta = 90^\circ, I = 0$ .

Thus, increasing the angle between the polarizer and analyzer reduces the intensity of transmitted light.

Write the condition for maximum intensity of light in a polarization experiment.

From Malus’s Law,

$I = I_0 \cos^2 \theta$

The intensity will be maximum when

$\cos^2 \theta = 1$

i.e., when

$\theta = 0^\circ$

Condition

Hence, if the transmission axes of the polarizer and analyzer must be parallel to each other, then:

$I = I_0$

How is Malus’s law used in everyday life?

Malus’s Law is used in many optical and practical applications, such as:

Optical stress analysis
Polarized sunglasses
3D movie glasses
Photography
LCDs

Explain how Malus’s law is used in the design of polarized sunglasses. How do these surfaces reduce glare from the reflective surface? Provide an example to illustrate your answer.

How Malus’s Law Is Used

According to Malus’s Law, polarized sunglasses work on the principle of selective transmission of light.

They contain a polarizing film that allows only light vibrating in one direction to pass through.

How They Reduce Glare

According to Malus’s Law, when the light falls on the reflective surface at a certain angle between the polarizer and analyzer, the reflected light intensity becomes almost zero, and glare is reduced.

$I = I_0 \cos^2 (90)$

$I = 0$

Example

When sunlight reflects off a lake’s surface, the reflected light is mainly horizontally polarized.

A person wearing polarized sunglasses (vertical axis) will see a much dimmer reflection, making the view through the water clearer and reducing eye strain.

What does Malus’s law state? Write the comprehensive mathematical derivation of the Malus Law.

Let!

$\mathbf{E}_0 = \text{electric field amplitude vector of incoming light}$
$\mathbf{A} = \text{vector along analyzer axis}$
$\theta = \text{the angle between } \mathbf{E}_0 \text{ and } \mathbf{A}}$ .

The component of the electric field along the analyzer’s axis is given by the dot product:

$A = \mathbf{E}_0 \cdot \hat{\mathbf{A}} = |\mathbf{E}_0| \cos \theta$

If,

the amplitude of the transmitted light = $A$
the amplitude of the incident light is $A_0 = |\mathbf{E}_0|$

Then,

$A = A_0 \cos \theta$

The intensity of light is proportional to the square of its amplitude:

$\text{intensity} \propto \text{amplitude}^2$

$\text{intensity} = k \text{amplitude}^2$

Before the analyzer:

$I_0 = k A_0^2$

After the analyzer:

$I_0 = k A^2$

$I = k (A_0 \cos \theta)^2$

$I = k A_0^2 \cos^2 \theta$

Dividing both equations:

$\frac{I}{I_0} = \cos^2 \theta$

Hence,

$\boxed{I = I_0 \cos^2 \theta}$

This is the Mathematical Form of Malus’s Law.

Malus’s Law and Comprehensive Mathematical Derivation of Malus Law | 101 Guide

Table of Contents

Introduction

Malus’s Law

Mathematical Formulation

Amplitude Relation

Intensity Relation

Before the Analyzer

After the Analyzer

Extreme Cases

Maximum Transmission

No Transmission

Conclusion

Frequently Asked Questions (FAQs)

State the Malus’s law. Explain the intensity formula.

What does happen to the intensity of light when it passes through a polarizer?

Write the effect of increasing the angle between the light wave and the analyzer on the intensity of light.

Write the condition for maximum intensity of light in a polarization experiment.

How is Malus’s law used in everyday life?

Explain how Malus’s law is used in the design of polarized sunglasses. How do these surfaces reduce glare from the reflective surface? Provide an example to illustrate your answer.

What does Malus’s law state? Write the comprehensive mathematical derivation of the Malus Law.

Leave a Comment Cancel Reply