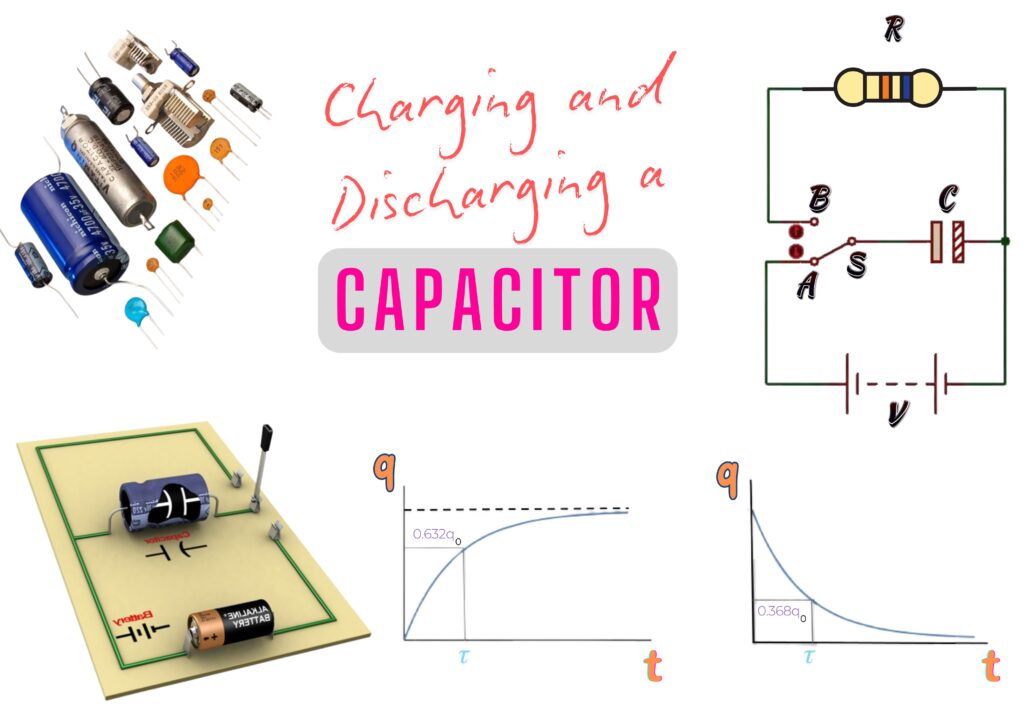
Charging and Discharging a Capacitor

Charging and Discharging a Capacitor | A Comprehensive Analysis of the 2wins Process

Leave a Comment / Blog / By

Charging and discharging a capacitor is a fascinating behaviour governed by exponential functions and is studied with the help of an RC circuit.

Introduction

Imagine a ceiling fan demonstrating the rotatory motion above us. When we turn it on, it does not instantly reach its full speed. Similarly, when we turn it off, it does not stop spinning immediately either— rather it slows down gradually. This behaviour can be compared to the charging and discharging of a capacitor in an RC circuit.

When a ceiling fan starts, its capacitor “charges” and provides the initial boost for the motor of the fan. Once the fan is running, the capacitor is no longer actively charging but helps stabilise the performance of the motor.

On the other hand, when the fan is turned off, the capacitor “discharges.” As a result, it releases stored energy to keep the fan running for a short time before it stops completely.

In an RC circuit, this process of gradual energy build-up (charging) and release (discharging) follows predictable patterns described by exponential equations. Understanding these principles is key to designing and analysing electronics like ceiling fans, timers, and signal processors.

Charging and Discharging behaviour of Capacitors

Capacitors, when paired with resistors, form RC circuits. An RC circuit is useful to understand the charging and discharging of a capacitor.

Charging a Capacitor

The commissioning of charges on a capacitor is called charging. Below are the essential details about charging a capacitor.

Process

When a capacitor is connected to a voltage source through a resistor, it begins to charge. The resistor limits the flow of current and causes the capacitor to accumulate charge gradually.

Charge Accumulation

The charge on the capacitor increases over time according to the given equation.

q(t) = q_0 \times (1 - e^{(-\frac{t}{\tau})})

q(t) = q_0 \times (1 - e^{(-\frac{t}{RC})})

Here,

  • q(t) = charge on the capacitor at time t
  • q_0 = maximum charge on the capacitor (q_0 = C \times V_0)
  • C = capacitance of the capacitor
  • R = resistance of the resistor
  • V_0 = maximum voltage of the source
  • \tau = time constant

Time Constant

The time constant represents the time taken by the capacitor to charge to approximately 0.63 (or 1 - \frac{1}{e}) times its equilibrium charge (also referred to as 63.2\% of its maximum charge)

It is equal to the product of resistance (R) and capacitance (C) and is given by,

\tau = R \times C

Voltage across Capacitor

The voltage across the capacitor during charging follows an exponential rise and is given as,

V(t) = V_0 \times (1 - e^{(-\frac{t}{\tau})})

V(t) = V_0 \times (1 - e^{(-\frac{t}{RC})})

Here,

  • q(t) = charge on the capacitor at time t
  • q_0 = maximum charge on the capacitor (q_0 = C \times V_0)
Key Points
  • Charging is not instantaneous. It follows an exponential curve.
  • After 5\tau, the capacitor is considered fully charged (99\% of maximum charge and voltage).
  • During charging, the current decreases exponentially as the capacitor opposes further charge build-up.

Discharging a Capacitor

The decommissioning of charges in a capacitor is called discharging. Below are the essential details about the discharging of a capacitor.

Process

When a charged capacitor is disconnected from the voltage source and connected to a resistor, it discharges its stored energy.

Charge Depletion

The charge on the capacitor decreases exponentially and is given as follows,

q(t) = q_0 \times e^{(-\frac{t}{\tau})}

q(t) = q_0 \times e^{(-\frac{t}{RC})}

Time Constant

The time constant remains the same (\tau = R \times C) and determines the rate of discharge.

Voltage across Capacitor

The voltage also decreases exponentially and is given as,

V(t) = V_0 \times e^{(-\frac{t}{\tau})}

V(t) = V_0 \times e^{(-\frac{t}{RC})}

Here,

  • V(t) = voltage across the capacitor at time t
  • V_0 = initial voltage across the capacitor
Key Points
  • Discharging also follows an exponential curve.
  • After 5\tau, the capacitor is effectively discharged, with the voltage and charge nearing zero.
  • Current flows in the opposite direction during discharge, gradually reducing to zero.

Visual Representation

Graphs of charging and discharging curves provide a clear visual representation of these processes. The charging curve shows an exponential rise towards the maximum voltage or charge, while the discharging curve shows an exponential decay towards zero.

What does “after 5\tau” mean?

\tau is the time it takes for significant change. For instance,

  • After 1\tau, about 63\% of charging/discharging is complete.
  • After 5\tau, the process is practically done (99\% charged or discharged).

This exponential behaviour reflects how capacitors manage energy in circuits, with \tau depending on the resistance (R) and capacitance (C) of the circuit.

Charging and Discharging a Capacitor | Practical Applications

RC circuits find widespread applications in various fields:

  • Timing Circuits: Used in devices like oscillators, delay circuits, and 555 timers.
  • Power Supply Smoothing: Capacitors help stabilise voltage in rectifiers, reducing ripple.
  • Energy Storage: Capacitors are used for temporary energy storage, such as in-camera flashes.
  • Signal Processing: Capacitors and resistors act as filters, allowing or blocking signals based on their frequency.

Conclusion

The charging and discharging behaviour of capacitors in RC circuits are governed by exponential functions and are strongly influenced by the time constant (\tau). Understanding these principles is essential for designing and analysing various electronic systems.

The time constant (\tau) plays a crucial role in determining the speed of charging and discharging. It represents the time taken for the capacitor to charge to approximately 63.2\% of its maximum charge or discharge to 36.8\% of its initial charge.

Frequently Asked Questions (FAQs)

What is an RC circuit?

An RC circuit consists of a resistor and a capacitor connected in series or parallel. It is used to analyse the charging and discharging behaviour of capacitors.

What does the time constant (\tau) signify?

The time constant, \tau = RC, is the product of resistance (R) and capacitance (C). It represents the time required for a capacitor to charge to 63.2\% of its maximum charge or discharge to 36.8\% of its initial charge.

Why does charging follow an exponential curve?

During charging, the voltage of a capacitor gradually approaches the source voltage due to the resistor limiting current flow. This results in an exponential rise in charge and voltage.

How long does it take for a capacitor to charge fully?

After 5\tau, a capacitor is considered fully charged (99\% of maximum charge and voltage).

What happens during capacitor discharge?

During discharge, the capacitor releases its stored energy through the resistor, causing its voltage and charge to decrease exponentially until near zero after 5\tau.

What are the practical applications of RC circuits?

RC circuits are used in,

  • Timing devices (oscillators, 555 timers)
  • Signal processing (filters)
  • Power supply smoothing
  • Energy storage systems

Can capacitors charge instantaneously?

No, capacitors cannot charge instantaneously due to the resistor limiting current flow. The charging process is gradual and follows an exponential curve.

How can I calculate the charge on a capacitor at any time t?

The following equations help determine the charge at any point during the charging and discharging of a capacitor.

  • During charging: q(t) = q_0 \times (1 - e^{-\frac{t}{RC}})
  • During discharging: q(t) = q_0 \times e^{-\frac{t}{RC}}

Leave a Comment

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.