Real-world examples in physics and engineering often involve variable forces, requiring precise calculations of work done. For this, work done by a variable force is determined using summation and integration methods.

Introduction

We know that what it means by work done by a constant force in physics. Now is the time to understand whether in the real world the work done remain the same irrespective of the force acting on it? Or do we use the average force to find the work done? The answer to these questions lie in the concept of variable force.

Variable Force

In many real-world scenarios, the force acting on an object does not remain constant throughout its motion. Such forces are known as variable forces.

These forces require a more detailed approach to calculate the work they perform.

Examples of Variable Forces

Gravity

The force of gravity acting on a rocket decreases as it moves farther away from Earth, following an inverse square relationship with the distance from the centre of Earth.

Springs

The force exerted by a spring increases as it is stretched beyond elastic limit, according to Hooke’s Law, $F = k x$ , where $k$ is the spring constant and $x$ is the displacement from equilibrium.

These examples highlight situations where forces change depending on position or distance, making it necessary to calculate work in a step-by-step manner.

Derivation of Work Done by a Variable Force

To calculate the work done by a variable force, divide the motion into small intervals, in such a way the force can be approximated as constant.

1. Divide the Path

Consider a particle moving from point ‘a’ to point ‘b’ along a curved path in the xy–plane, and the curved path is divided into small equal intervals as shown.

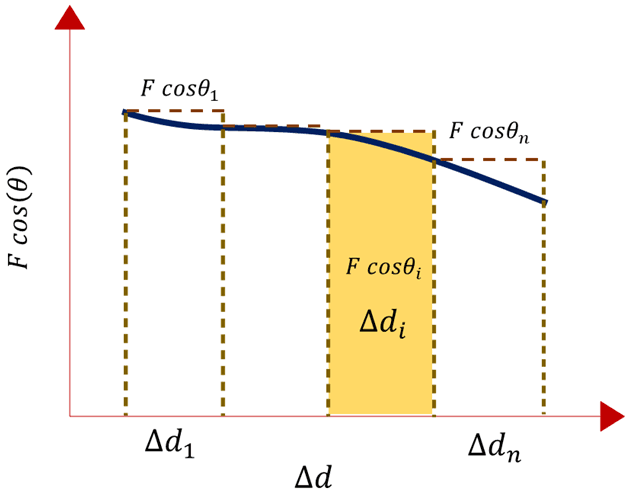
Derivation of Work Done by a Variable Force

2. Approximate Force and Displacement

The force acting along each path is constant, i.e.,

$F_i \quad \to \quad F_1, F_2, …, F_n$

The corresponding path is also divided into small intervals of displacement, i.e.,

$\delta d_i \quad \to \quad \delta d _1, \delta d _2, …, \delta d _n$

3. Work Done in Each Interval

We know that the work done is calculated as follows,

$W = F d \cos \theta$

Here, $W$ represent the work done by the force.

For 1^st Interval

$W_1 = F_1 \delta d_1 \cos \theta_{1}$

For 2^nd Interval

$W_2 = F_2 \delta d_2 \cos \theta_{2}$

For n^th Interval

$W_n = F_n \delta d_n \cos \theta_{n}$

4. Total Work Done

The total work done is the sum of the work in all intervals, given as,

$W = \sum_{i=1}^{n} W_i$

$W = W_1 + W_2 + … + W_n$

$W = F_1 \delta d_1 \cos \theta_{1} + F_2 \delta d_2 \cos \theta_{2} + … + F_n \delta d_n \cos \theta_{n}$

$W = \sum_{i=1}^{n} F_i \delta d_i \cos\theta_{i}$

Graphical Representation of Work Done by a Variable Force

A graphical method can also be implemented to visualise the work done by a variable force.

Plot $F\cos\theta$ vs. Displacement

Consider the graph plotted against the effective component of force $F_x$ and the displacement $d$ as shown.

Graphical Representation of Work Done by a Variable Force

The path is divided into small intervals, and is assumed constant in each interval.

Area under the Graph Line

Each shaded rectangle in the graph represent the work done in the $i^{\text{th}}$ interval, and given as,

$\text{Work Done} = \text{Area of the Rectangle}$

$W_n = A_n$

$W_n = \left(F_n \cos \theta_{n}\right) \delta d_n$

Here,

$W_n$ = work done in the $n^{\text{th}}$ interval
$A_n$ = area of rectangle in the $n^{\text{th}}$ interval
$n = 1, 2, 3, …$

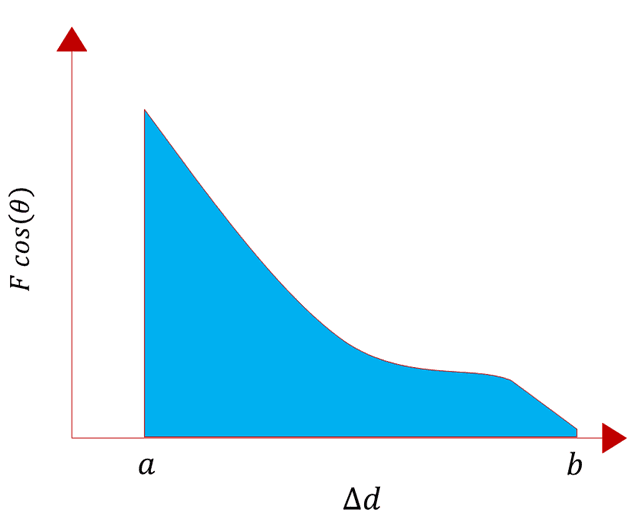
Total Area as Work

The total work done is equal to the sum of the areas of all rectangles.

$W = \sum_{i=1}^{n} A_i$

$W = A_1 + A_2 + … + A_n$

Here, $A_1, A_2, …, A_n$ are area of small rectangles.

This method provides an intuitive way to understand work as the area under the $F\cos\theta-\text{vs} d$ curve.

Limit of Small Intervals

Smaller Intervals, Greater Accuracy

As the size of each displacement interval $\left(\delta d\right)$ becomes smaller, the approximation of constant force within each interval becomes more accurate. When $\delta d$ approaches zero, the number of intervals increases infinitely.

Area under the Curve

In the limit where $\delta d$ approaches zero, the sum of the rectangular areas becomes the exact area under the curve. Mathematically, this is represented by integration. This integral gives the precise value of work done by the variable force over the entire path.

Conclusion

The work done by a variable force in moving a particle between two points is equal to the area under the $F\cos\theta - \text{vs} - d$ . This idea is fundamental in physics and engineering, providing a way to analyse systems where forces vary with position, such as in gravitational fields, elastic systems, and more.

Frequently Asked Questions (FAQs)

What is a variable force?

A variable force is a force that changes in magnitude or direction as an object moves, unlike a constant force, which remains unchanged.

Why is work done by a variable force different from a constant force?

In the case of a constant force, work is calculated using a simple formula:

$W = F d \cos\theta$

However, for a variable force, the force changes over distance, requiring summation or integration to determine the total work done.

What are some real-world examples of variable forces?

Examples include:

Air resistance acting on a moving object
Gravitational force on a rocket moving away from Earth
The force exerted by a stretched or compressed spring (Hooke’s Law)

How do we calculate work done by a variable force?

The work done is found by dividing the motion into small intervals where the force is approximately constant. The total work is obtained by summing the work done in each small interval or by integrating the force over the displacement.

What is the significance of the area under the force-displacement curve?

The area under the $F\cos\theta$ vs. displacement graph represents the total work done by the variable force. The smaller the intervals, the more accurate the approximation.

Why do we use integration in calculating work done by a variable force?

As the number of intervals approaches infinity, the summation of work done in each interval turns into an integral, which provides an exact calculation of the work done.

What is the mathematical expression for work done by a variable force?

The work done is given by:

$W = \int_a^b F \cos\theta \, d$

Here,

$F$ = force
$d$ = displacement
$\theta$ = angle between force and displacement

How does Hooke’s Law relate to work done by a variable force?

Hooke’s Law states that the force exerted by a spring is proportional to its displacement:

$F = kx$

Since this force varies with displacement, the work done in stretching or compressing a spring requires integration.

What happens when the displacement interval approaches zero?

When the displacement interval becomes infinitely small, the work done is calculated precisely using integration, eliminating approximation errors.

Why is the study of work done by variable forces important in physics and engineering?

Understanding work done by variable forces is crucial in fields like aerospace, mechanical engineering, and biomechanics, where forces change with position, such as in gravitational fields, elasticity, and frictional systems.

Master Derivation of Work Done by a Variable Force | BISE 1st Year

Table of Contents

Introduction

Variable Force

Examples of Variable Forces

Derivation of Work Done by a Variable Force

1. Divide the Path

2. Approximate Force and Displacement

3. Work Done in Each Interval

4. Total Work Done

Graphical Representation of Work Done by a Variable Force

Area under the Graph Line

Total Area as Work

Limit of Small Intervals

Smaller Intervals, Greater Accuracy

Area under the Curve

Conclusion

Frequently Asked Questions (FAQs)

What is a variable force?

Why is work done by a variable force different from a constant force?

What are some real-world examples of variable forces?

How do we calculate work done by a variable force?

What is the significance of the area under the force-displacement curve?

Why do we use integration in calculating work done by a variable force?

What is the mathematical expression for work done by a variable force?

How does Hooke’s Law relate to work done by a variable force?

What happens when the displacement interval approaches zero?

Why is the study of work done by variable forces important in physics and engineering?

Leave a Comment Cancel Reply