Here we shall learn about force-momentum relationship as well as Impulse and their real-life applications and mathematical explanations.

Introduction

Understanding force, momentum, and impulse, and their relationship are important aspects of a moving object. They are crucial for analysing how objects move and interact in our world. They form the foundation of dynamics and provide insights into everything we witness around us.

Force-Momentum Relationship and Impulse

These concepts are essential as they provide us with a quantitative way to determine them.

What is Force?

Force (F) is any interaction that causes a push or a pull on an object either to accelerate or decelerate it, change its direction, or deform it. It can stop a moving object or can start a stationary object. It is given as,

$F = m a$

To know more about it click here.

What is Momentum?

Momentum (p) can be thought of as the quantity of motion of an object and depends on both its mass and velocity. The greater the mass and/or velocity of an object, the greater its momentum. It is given as,

$p = m v$

To know more about it click here.

Force-Momentum Relationship

The two physical quantities (F and p) are closely related in the study of dynamics (more specifically, kinetics). Their relationship is based on the Newton’s 2^nd law of motion, however, expressed in terms of momentum.

In this case, it can be stated as,

“The change in momentum of an object is directly related to the force applied to it and the time over which the force is applied.”

Mathematical Formulation

Consider a car accelerating from A to B in a certain time and experiencing a force as shown.

According to Newton’s 2^nd law of motion,

$F = m a$

From the definition of acceleration,

$a = \frac{\Delta v}{\Delta t}$

$a = \frac{v_f - v_i}{\Delta t}$

Now, we can express 2^nd law of motion as follows:

$F = m \cdot \frac{v_f - v_i}{\Delta t}$

$F = \frac{mv_f - mv_i}{\Delta t}$

From the definition of momentum,

$p = m v$

Hence, the force becomes,

$F = \frac{p_f - p_i}{\Delta t}$

$F = \frac{\Delta p}{\Delta t}$

This equation forms the foundation for understanding how forces cause changes in momentum.

What is Impulse?

It can be defined as,

“the total effect of a force acting over time.”

“the product of force and the change in time.”

“the change in momentum of an object when a force is applied.”

“a large amount of force acting for a short interval of time (or vice versa).“

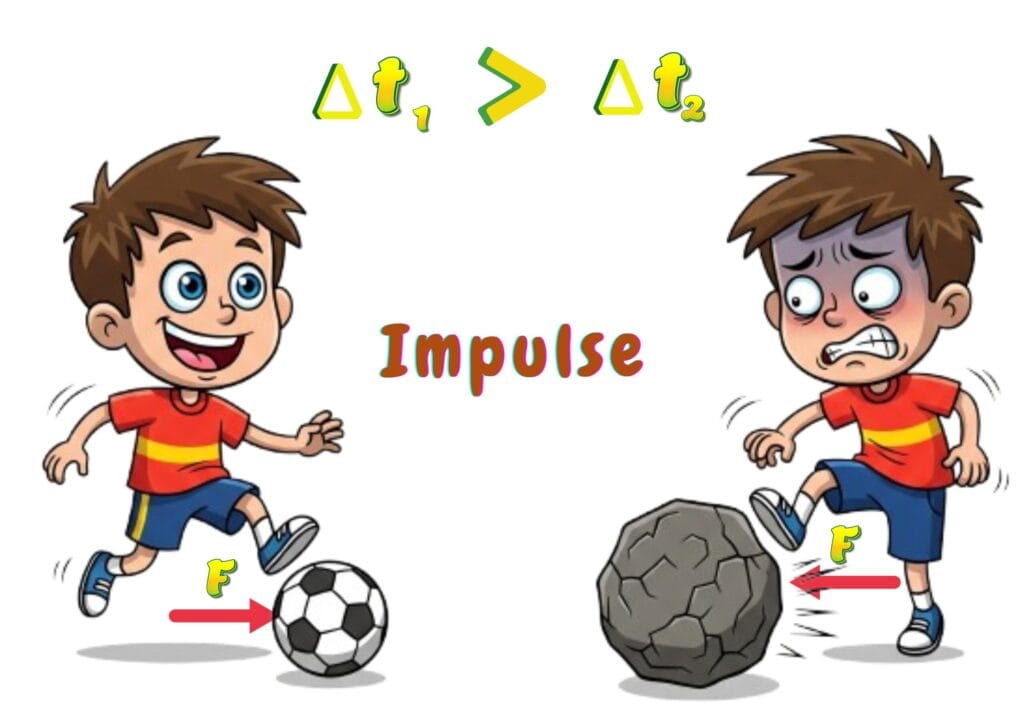
Key Properties of Impulse

Some of its key properties are given below.

Representation

It is usually represented by the symbol J.

Unit

In the International System of Units, it is measured in newton-second (Ns).

Type of Quantity

It is classified as a derived quantity SI system.

Nature of Quantity

It is a vector quantity that requires both magnitude and direction.

Mathematical Formulation

Mathematically, it is given by the equation:

$J = F \cdot \Delta t$

Where,

$J$ = impulse
$F$ = force
$\Delta t$ = time interval (during which the force acts)

It can also be represented in terms of change in momentum.

$J = \Delta p$

This shows that impulse is also equal to the change in momentum.

Significance of Impulse

It is especially important when analysing collisions or interactions where forces are applied over short periods. It helps explain why a softer or slower impact can be less damaging than a fast, sharp collision.

Physical Meaning of Impulse

It quantifies the effects of forces over time, and thus, helps us to reduce or amplify the severe impact on an object.

For instance, during a collision (as in the case of a car crash or a parachutist descent), the force applied is typically very large but acts over a short time.

The impulse imparted during the collision results in a change in the momentum of the object. The greater the impulse, the larger the change in momentum and the greater the impact force.

However, if the impulse can be spread over a longer time (as with airbags or parachutes), the force can be reduced and the damage can be minimised.

Conclusion

In a nutshell, force, momentum, and impulse are interconnected concepts that help us understand motion and interaction in the physical world.

Force is the cause of changes in motion, measured as the product of mass and acceleration, while, momentum quantifies the motion of an object and is dependent on its mass and velocity.

The relationship between force and momentum is expressed through impulse. It is the total effect of force acting over time that causes the change in momentum of an object. This relationship allows us to calculate how forces affect momentum in different scenarios.

Understanding these fundamental principles allow us to analyse and predict the behaviour of objects under various conditions in the real world.

Frequently Asked Questions (FAQs)

What is the difference between force and momentum?

Force is an interaction that causes a change in the motion of an object, while momentum measures the motion of an object based on its mass and velocity.

Force is the rate of change of momentum over time, expressed as $F = \frac{\Delta p}{\Delta t}$ , where $\Delta p$ is the change in momentum and $\Delta t$ is the time interval.

What is the significance of impulse in real-life applications?

It helps explain the effects of forces acting over time, such as reducing impact forces in car crashes with airbags or increasing time for force application in sports like cricket or baseball.

It is equal to the change in momentum of an object, expressed as $J = \Delta p$ .

What are the units of force, momentum, and impulse?

Force: Newton (N)
Momentum: Kilogram meter per second (kg m/s)
Impulse: Newton-second (Ns)

What happens to momentum during a collision?

During a collision, momentum is conserved in a closed system unless an external force acts on it. The momentum before and after the collision is equal.

Can an object have momentum without force acting on it?

Yes, an object in motion continues to have momentum even if no force acts on it (Newton’s first law), provided there is no resistance or opposing force.

Why is impulse important in designing safety equipment?

Safety equipment like airbags and helmets increase the time of force application during an impact, reducing the force experienced and minimizing injury.

What factors affect the momentum of an object?

Momentum depends on the mass and velocity of an object, as described by $p = m v$ .

How does changing the time duration of a force affect impulse?

Increasing the time duration over which a force acts spreads out the impact, reducing the force and potentially lessening the damage, while still resulting in the same impulse.

Understanding Force-Momentum Relationship and Impulse | 2 Concept in A Comprehensive Guide

Table of Contents

Introduction

Force-Momentum Relationship and Impulse

What is Force?

What is Momentum?

Force-Momentum Relationship

Mathematical Formulation

What is Impulse?