How to solve simultaneous linear equations? Here, we shall learn about 5 effective techniques to solve simultaneous linear equations (SLEs) with clear steps.
Table of Contents
Introduction
We know that Simultaneous Linear Equations (SLEs) are important in our lives as they assist us in solving problems where multiple conditions need to be satisfied at the same time.
It is a system of equations that contains two or more same variables. All these equations satisfy either one or more set of numbers which are written as ordered pair and called as solution set. The number of equations in the system, in order to find the solution, should be equal to the number of variables involved.
What Are Simultaneous Linear Equations (SLEs)?
The Equations of the form:
![\[a_1x + b_1y = c_1\quad\quad…\quad\quad(1)\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-72f0c2e626f42645ad56f3aa52dfacf7_l3.png "Rendered by QuickLaTeX.com")
![\[a_2x + b_2y = c_2\quad\quad…\quad\quad(2)\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-5c68bf5cda694345088c0c9bd218aed9_l3.png "Rendered by QuickLaTeX.com")
are called the system of simultaneous linear equations in two variables.
Similarly, the equations of the form:
![\[a_1x + b_1y + c_1z = d_1\quad\quad…\quad\quad(i)\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-e8a75773c20ef98511d1c04d39f77921_l3.png "Rendered by QuickLaTeX.com")
![\[a_2x + b_2y + c_2z = d_2\quad\quad…\quad\quad(ii)\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-d871a6f61a0a312b696ca53b05fb97a6_l3.png "Rendered by QuickLaTeX.com")
![\[a_3x + b_3y + c_3z = d_3\quad\quad…\quad\quad(iii)\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-3381ba2593424095d0fc5ebc1fdcfa24_l3.png "Rendered by QuickLaTeX.com")
are called as the system of simultaneous linear equations in three variables.
There are certain ways to find the solution of simultaneous linear equations. Below, we shall talk about all those methods.
How to Solve Simultaneous Linear Equations? 5 Effective Methods
There are different ways to solve a system of SLEs. If we want to excel in the field of STEM, we need to learn how to solve simultaneous linear equations. However, only the five most fundamental methods to solve simultaneous equations are discussed here. Now, let us learn how to find the solution of system of equations.
1. Graphical Method
The graphical method involves plotting both equations on a coordinate plane and finding the point where the two lines intersect. This point of intersection represents the solution to the SLEs.
Steps Involved
Rearrange each equation, (1) and (2), into the form y = mx + c (slope-intercept form) for easier graphing.
For the equation (1):
![\[y = \frac{c_1 - a_1x}{b_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-b47beec5d328411bf105eafd8cb75170_l3.png "Rendered by QuickLaTeX.com")
![\[y = \frac{c_1}{ b_1} - \frac{a_1x}{b_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-d7e023c42804c9917c2de2cc668c6182_l3.png "Rendered by QuickLaTeX.com")
![\[y = - \frac{a_1}{b_1}x + \frac{c_1}{ b_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-9c6394923cbf88c97671026b306b0212_l3.png "Rendered by QuickLaTeX.com")
For the equation (2):
![\[y = \frac{c_2 - a_2x}{b_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-abd8c4cb9662669ad66caa295d670c50_l3.png "Rendered by QuickLaTeX.com")
![\[y = \frac{c_2}{ b_2} - \frac{a_2x}{ b_2}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-f1370ae3bfbc19e37b1e1b30d824715d_l3.png "Rendered by QuickLaTeX.com")
![\[y = - \frac{a_2}{b_2}x + \frac{c_2}{b_2}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-9f8997af40ce05f3cb9dc514d1ff1fb0_l3.png "Rendered by QuickLaTeX.com")
Plot the two lines by selecting convenient values for x, and then calculate the corresponding y values. One convenient way to do this task, which is applicable in most of the situation, is shown below.
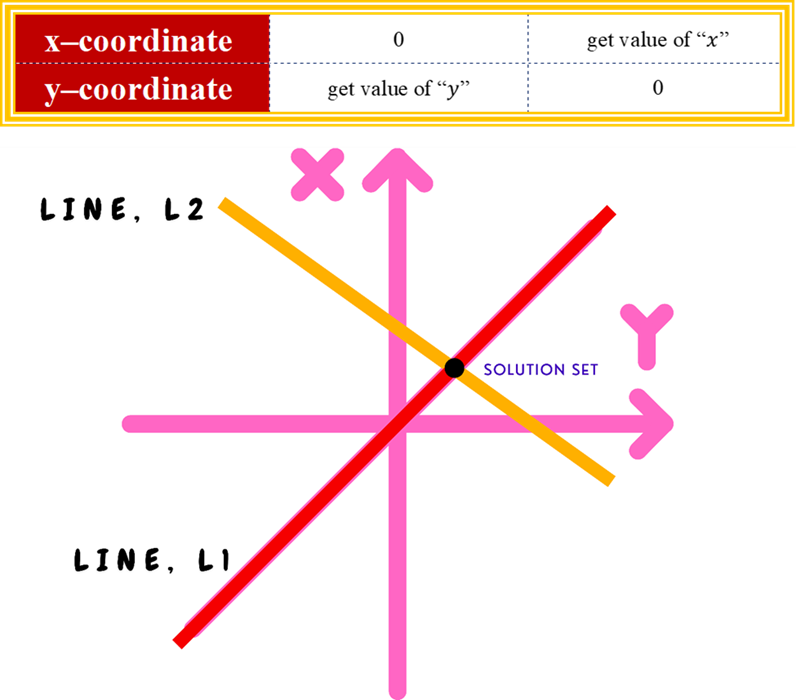
The point of intersection is the solution (x, y).
Note, both lines are plotted separately according to a chosen scale. For this, we must have the knowledge about Cartesian coordinate system, its elements, and the way it works. If the lines are parallel, there is no solution. If the lines coincide, there are infinitely many solutions.
2. Substitution Method
In this method, one equation is solved for in terms of one variable, and then substituted into the second equation.
Steps Involved
Solve the equation (1) for x or y. For example, solving for x:
![\[x = \frac{c_1 - b_1y}{a_1} \quad\quad \text{(assuming } a_1 \neq 0\text{)}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-c18c9551c95b46f5730f1b0341f29249_l3.png "Rendered by QuickLaTeX.com")
Substitute this expression for x into the equation (2):
![\[a_2\left(\frac{c_1 - b_1y}{a_1}\right) + b_2y = c_2\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-3e28e7e1108d8b4632997ff518824d38_l3.png "Rendered by QuickLaTeX.com")
Solve the resulting equation for y:
![\[y = \frac{a_2c_1 - a_1c_2}{a_2b_1 - a_1b_2}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-99885c07ce104b517895daf95cb17b7b_l3.png "Rendered by QuickLaTeX.com")
Substitute the value of y back into the equation (2) to find the value of x:
![\[a_2x + b_2(\frac{a_2c_1 - a_1c_2}{a_2b_1 - a_1b_2}) = c_2\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-0bd17351f757e8ab1ad20e74a332da58_l3.png "Rendered by QuickLaTeX.com")
![\[x = \frac{(b_1c_2 - b_2c_1)}{(a_1b_2 - a_2b_1)}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-4b995a495f036b50c48bb94f60c1f575_l3.png "Rendered by QuickLaTeX.com")
3. Elimination Method
The elimination method involves first making coefficient of equation the same and then adding or subtracting the equations in such a way that one variable cancels out, leaving an equation with single variable to solve.
Steps Involved
Multiply both equations by suitable constants to make the coefficients of either x or y the same. For example, if we want to eliminate x, multiply equation (1) by a2 and equation (2) by a1.
![\[a_2(a_1x + b_1y) = a_2c_1 \quad\quad\quad \Rightarrow \quad\quad\quad a_1a_2x + a_2b_1y = a_2c_1\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-01bdc068149d388ac0d9d8b8e061096a_l3.png "Rendered by QuickLaTeX.com")
![\[a_1(a_2x + b_2y) = a_1c_2 \quad\quad\quad \Rightarrow \quad\quad\quad a_1a_2x + a_1b_2y = a_1c_2\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-14d8cb281ce30d13e32c013f200ae320_l3.png "Rendered by QuickLaTeX.com")
Subtract the two equations to eliminate x:
![\[(a_1a_2x + a_2b_1y) - (a_1a_2x + a_1b_2y) = a_2c_1 - a_1c_2\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-efdcdb5718541b437c21fa52a45844e3_l3.png "Rendered by QuickLaTeX.com")
Solve for y by expanding and simplifying:
![\[(a_2b_1 - a_1b_2)y = a_2c_1 - a_1c_2 \]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-38a5b2e00b77115f282b228adb7a9034_l3.png "Rendered by QuickLaTeX.com")
Substitute the value of y into the equation (2) to find x:
4. Cross Multiplication Method
The cross multiplication method provides a direct formula-based approach to solving simultaneous linear equations in two variables.
Steps Involved
Write the system of equations:
![\[\frac{x}{b_1c_2 - b_2c_1} = \frac{y}{c_1a_2 - c_2a_1} = \frac{1}{a_1b_2 - a_2b_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-0f32dc0a289646d2e2baa8783f9c9a87_l3.png "Rendered by QuickLaTeX.com")
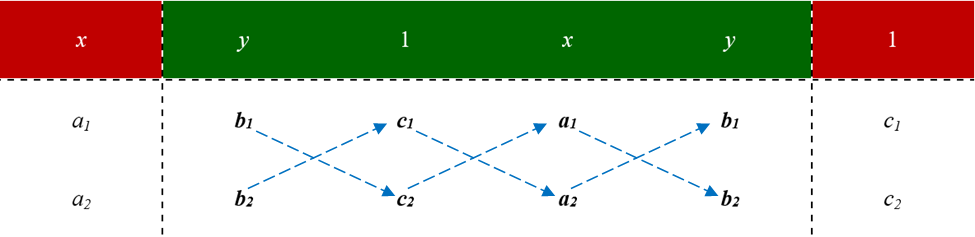
Set up the equal ratios:
![\[\frac{x}{b_1c_2 - b_2c_1} = \frac{1}{a_1b_2 - a_2b_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-02d07ac18496ad7076317f9dc3b201e7_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{y}{c_1a_2 - c_2a_1} = \frac{1}{a_1b_2 - a_2b_1}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-367b3c7b22e220148b1b2c2d2b15fe45_l3.png "Rendered by QuickLaTeX.com")
Solve for the values of x and y:
![\[y = \frac{(c_1a_2 - c_2a_1)}{(a_1b_2 - a_2b_1)}\]](https://contentxseed.com/wp-content/ql-cache/quicklatex.com-a1b2b3191357b9e98a1180e766ded8a2_l3.png "Rendered by QuickLaTeX.com")
5. Matrix Method
The matrix method uses matrix algebra to solve SLEs by expressing the system as A X = B, where A is the matrix of coefficients, X is the column vector of variables, and B is the constant vector. The matrices are solved either with direct or iterative method.
Direct Method – Matrix
Direct methods for solving systems of linear equations (SLEs) provide a solution in a finite number of steps, as opposed to iterative methods that gradually converge to a solution.
A list of the direct methods that are commonly used are:
- Matrix Inversion (Inverse Method)
- Cramer’s Rule
These two are the most fundamental methods to solve problems related to SLEs. Other direct methods include:
- Gaussian Elimination
- Gauss-Jordan Elimination
- LU Decomposition (LU Factorization)
- Cholesky Decomposition
- Block Matrix Method
- Schur Complement
Key Characteristics of Direct Methods:
- Exact solution: (barring round-off errors in numerical computations)
- Finite steps: (unlike iterative methods that continue until convergence)
- Efficiency: (efficient for smaller or moderately sized systems)
Common Use Cases
- The system is relatively small or moderate in size.
- The coefficient matrix is dense (as opposed to sparse).
- An exact solution is required without approximation.
- The matrix has a specific structure (e.g., symmetric or triangular).
These methods are good tools to solve problems related to the linear algebra and are used in fields like physics, engineering, computer graphics, and numerical analysis.
Conclusion
To learn how to solve simultaneous linear equations is essential for tackling problems in the fields like engineering, physics, and economics.
Each of these methods—Graphical, Substitution, Elimination, Cross Multiplication, and Matrix—offers a unique approach depending. It depends on the complexity of the problem and the required precision.
While graphical methods provide a pictorial view, algebraic methods like substitution and elimination offer direct solutions.
The matrix method, compared with algebraic methods, are advanced techniques that are widely used in computation where larger systems are involved. This method provides efficiency in the complex problems of engineering and technology.
Mastering all these techniques is a good thing as they enhance our problem-solving skills. They make us more skilled at handling real-life situations where multiple variables are involved.
Frequently Asked Questions (FAQs)
How does the graphical method work?
In the graphical method, each equation is plotted on a coordinate plane, and the point where the lines intersect gives the solution for the variables.
What is the substitution method?
The substitution method involves solving one equation for a variable and substituting that expression into the other equation to find the remaining variable.
Can you explain the elimination method?
The elimination method involves adding or subtracting equations to eliminate one variable, allowing for easier solving of the remaining equation.
What is the cross multiplication method?
This method uses a specific formula to express the solutions of the equations directly and is particularly useful for quick calculations.
How does the matrix method work?
The matrix method represents the system of equations in matrix form and uses matrix algebra to find the solutions by calculating the inverse of the coefficient matrix.