The comprehension of the place values and number forms build a strong mathematical foundation—for today and the future!
Table of Contents
Introduction
Since kindergarten, you have seen 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Do you know what these are?
These are called digits!
Each digit gives us a piece of information in terms of its value. Once you understand what each digit represents based on its position, you can confidently read, write, and interpret numbers in various forms. These forms include:
- numeric (digit) form
- verbal (word) form
- expanded form
- normal form
Understanding how numbers work is essential in mathematics. It starts with a simple but powerful idea: place value.
1. What is a Place Value?
Place value is the value a digit holds because of its position in a number. For example:
- In 1952, the digit 9 is in the hundreds place → 900
- In 9125, the same 9 is in the thousands place → 9000
Notice that even though it is the same digit, its value changes depending on its position. That is what place value is all about.
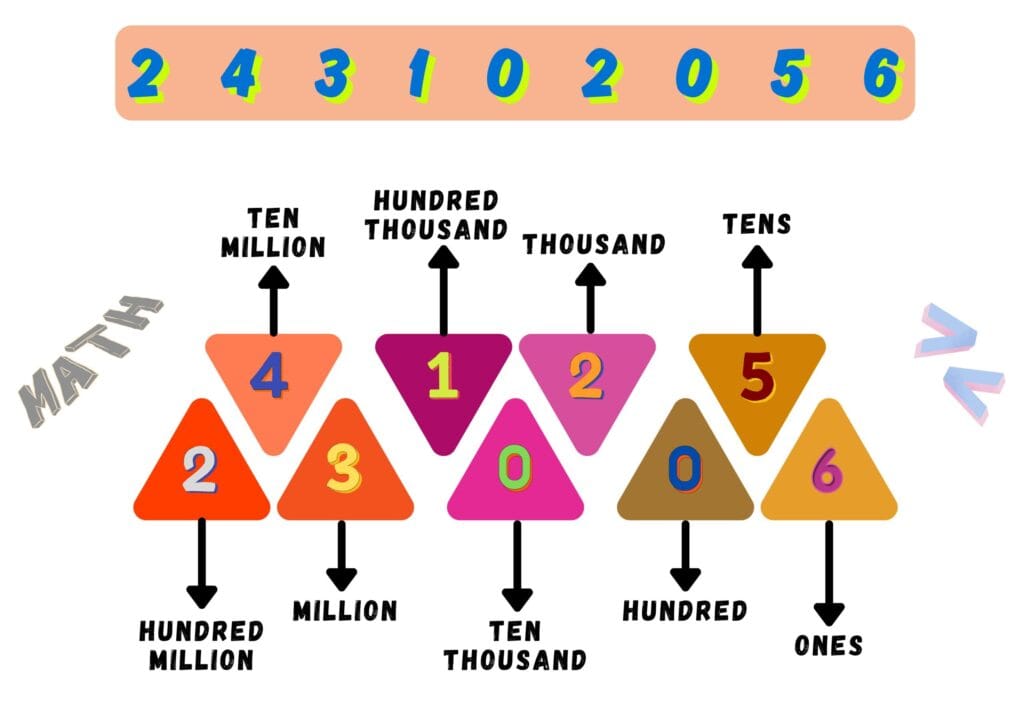
How Place Value Is Structured
There are two common ways to group digits in large numbers. Each is based on how commas are placed and how digits are read.
a) English (International) Method
Digits are grouped in sets of three, starting from the right.
b) South Asian (Subcontinent) Method
Here, the first group is three digits from the right, and after that, commas are placed every two digits.

For this explanation, we shall focus on the English method, which is used in most international settings.
Key Tip to Remember
Digits are read according to their place meaning, recite the number first followed by the place value. For example, in 1952:
- For thousands → 1 thousand (full name)
- For hundreds → 9 hundred (full name)
- For tens → fifty (use “–ty” words)
- For ones → two (just say the digit name)
Note that zero is not read in any place value, however, it remains a mandatory part of that place.
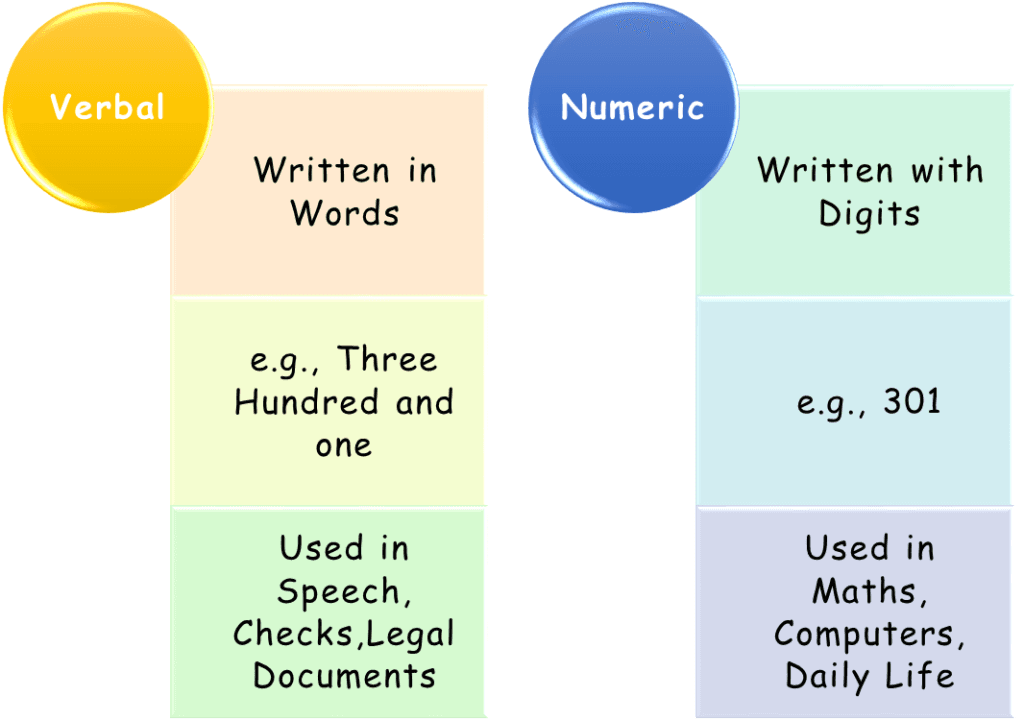
2. Verbal Form vs. Numeric Form
A number can be written in two basic ways:
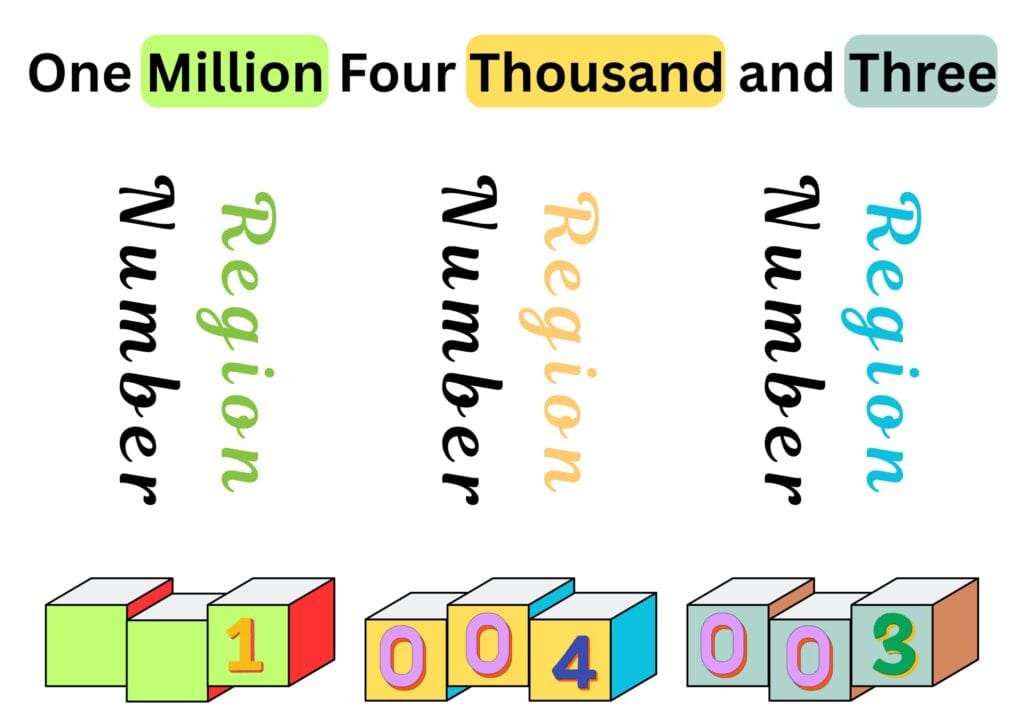
Converting Numbers to Words
- Group digits into sets of three (regions): units, thousands, millions
- Read each group like a 3-digit number
- Add the region name (thousand, million, etc.)
- Skip any region that’s all zeros.
- Use “and” after hundreds (especially in British English)

Notes
- Skip values of zero (e.g., don’t say “zero hundred”)
- Tens are read as “–ty” words (twenty, thirty)
- “And” is common in British/Australian usage and optional in American English.
Converting Words to Numbers
- Break the sentence into regions (millions, thousands, units)
- Read the number in each region
- Convert each to digits (up to 3 per group)
- Combine in the correct order
- Add zeros where a place is skipped
If a place is not mentioned (e.g., no “hundreds”), assume zero.
3. Normal Form vs. Expanded Form
A number can either be represented in the usual way or be broken down into its place values. Based on this we have two forms of numbers.

Converting Normal to Expanded
Consider a number in its normal form: 320,192. To convert it into an expanded form.
320,192 = 3 × 100,000 + 2 × 10,000 + 0 × 1000 + 1 × 100 + 9 × 10 + 2
OR
320,192 = 300,000 + 20,000 + 0 + 100 + 90 + 2
OR
320,192 = 300,000 + 20,000 + 100 + 90 + 2
Note, the 0 in hundred-thousand is skipped for neatness.
Converting Expanded to Normal
Consider a number in its expanded form: 700 + 50 + 4. To convert it into normal form.
700 + 50 + 4 = 754
Similarly, for a number like 900,000 + 20,000 + 10 + 9, the normal form is found by filling the missing values – thousands and hundreds.
900,000 + 20,000 + 0 + 0 + 10 + 9 = 920,019
Why Use Different Forms?
Switching between different forms improves number sense, communication, and confidence in math.
| Form | Purpose |
| Verbal | For speech, writing, checks, legal docs |
| Numeric & Normal | For calculations, computers, records |
| Expanded | To understand number structure and digit value |
Conclusion
Mastering number and number system (numeric representation) is not just for exams. It is a lifelong tool for thinking clearly about numbers, solving problems, and making decisions.
These skills are used not just in school, but in real life—from reading bills to writing checks.
Place value shows what each digit means based on position. Different forms of numbers serve different purposes. Being able to convert between forms is a key math skill.
Frequently Asked Questions (FAQs)
What is place value, and why is it important?
Place value can be defined as “the value of a digit based on its position within a number.”
What is the difference between the verbal form and the standard form of numbers?
Verbal form refers to stating a number in words, while standard form denotes the number using digits (numeric notation).
For instance, the number “256” in verbal form is “two hundred fifty-six.”
What is the normal form of a number?
The normal form of a number is the usual way of representing a number. For instance, 1234, etc.
What is the expanded form of a number?
Expanded form refers to the breaking down of a number into pieces and writing them as the summation of its place values.
For example, the number 420 in its expanded form is 400 + 20 + 0.
How does understanding of place values and number forms help us in real life?
Understanding place value and numeric representation is essential in everyday activities. For instance: shopping, keeping track of scores in any sport, and understanding measurements. It enables clear communication and efficient problem-solving.

