Understanding the differences between reflection of light and refraction of light, the 2 important light behaviours, provides an essential foundation for studying optics and the wave nature of electromagnetic radiations.
Table of Contents
Introduction
Previously, you explored what light is and how it behaves. Now let us see what happens when light meets a surface or a new medium.
Light follows a simple rule;
Travel in straight lines, bend and/or bounce on collision.
Light rays travel in a straight path and are called as parallel beam of rays. Moreover, the two behaviours bouncing off and bending are linked with reflection and refraction of light. The phenomena – reflection and refraction of light – are the foundation of:
- Lenses
- Mirrors
- Glasses
- Cameras
- Optical Effects

Reflection of Light
Reflection is the change in direction of a light ray at a surface so that the ray returns into the medium from which it came. Simply:
Light hits a surface and bounces back.
Laws of Reflection
The law of reflection can easily be explained with two clear, testable rules:
- The angle of incidence equals the angle of reflection measured from the normal (an imaginary line perpendicular to the surface).
- The incident ray, the reflected ray, and the normal all lie in the same plane.
The few terms that needs to be addressed here are:
- Angle of Incidence (∠i) → the angle formed between the incident ray (the incoming ray of light) and the normal at the point of incidence.
- Angle of Reflection (∠r) → the angle formed between the reflected ray (the ray that bounces off the surface) and the normal.
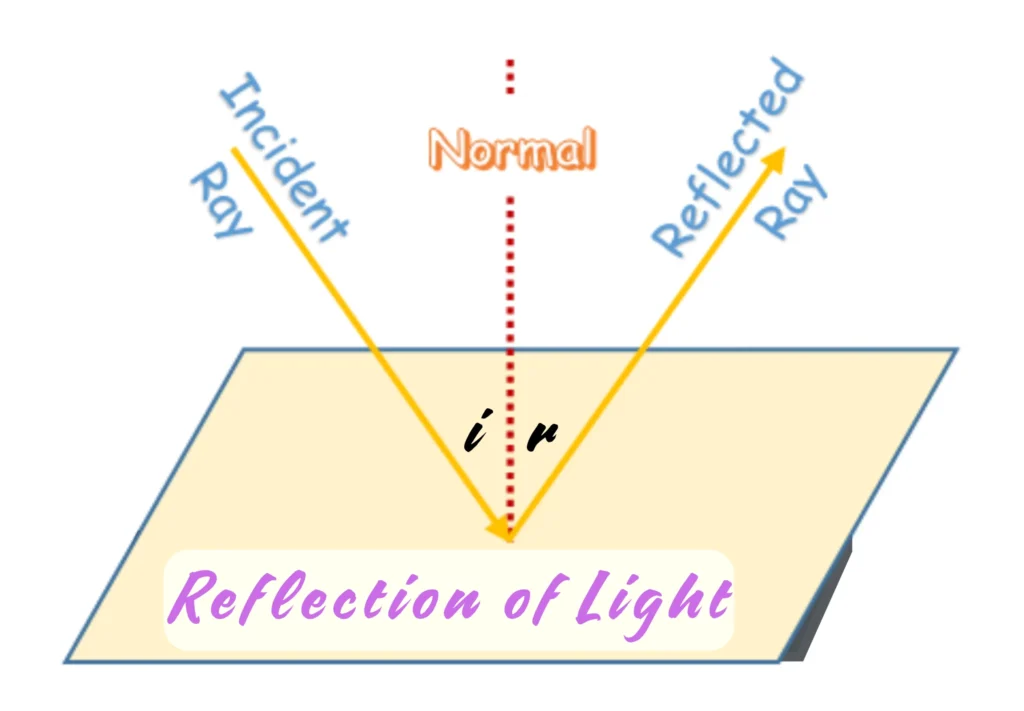
- Normal → an imaginary line drawn perpendicular (at 90°) to the surface at the exact point where the incident ray strikes. It acts as a reference line for measuring the angles of incidence and reflection.
- Same Plane → all lines lie on a single flat surface (or geometric plane) and neither of them deviate out of that plane.
Understanding of this law let you predict exactly where an image will appear in a mirror.
Types of Reflection
Not all surfaces reflect light the same way. Based on this fact, there are 2 types of reflection:
Regular (Specular) Reflection
It happens on smooth, shiny surfaces like mirrors, still water, and polished metal. Parallel incoming rays remain parallel after reflection, producing clear images and bright glints.
Diffuse (Irregular) Reflection
It happens on rough surfaces like paper, cloth, and unpolished wood. Due to uneven bumps, incoming parallel rays scatter in many directions at the point of incidence.
Diffuse reflection is why you can see non-shiny objects from many angles.
Simple Experiments
Here are simple, fun ways to see reflection in action:
- Mirror-and-ray-diagram demo: Place a small card with a drawn arrow in front of a plane mirror. Use a laser pointer (or a narrow flashlight beam) to draw the incident ray and the reflected ray on paper. Measure the angles with a protractor — you’ll see incidence = reflection.
- Periscope: Two mirrors placed at 45° in a box let you see over obstacles. The beam reflects off two mirrors and reaches your eye — practical reflection in action!
- Kaleidoscope: Multiple reflections between angled mirrors create repeating patterns. It’s a playful application of specular reflection and symmetry.
Refraction of Light
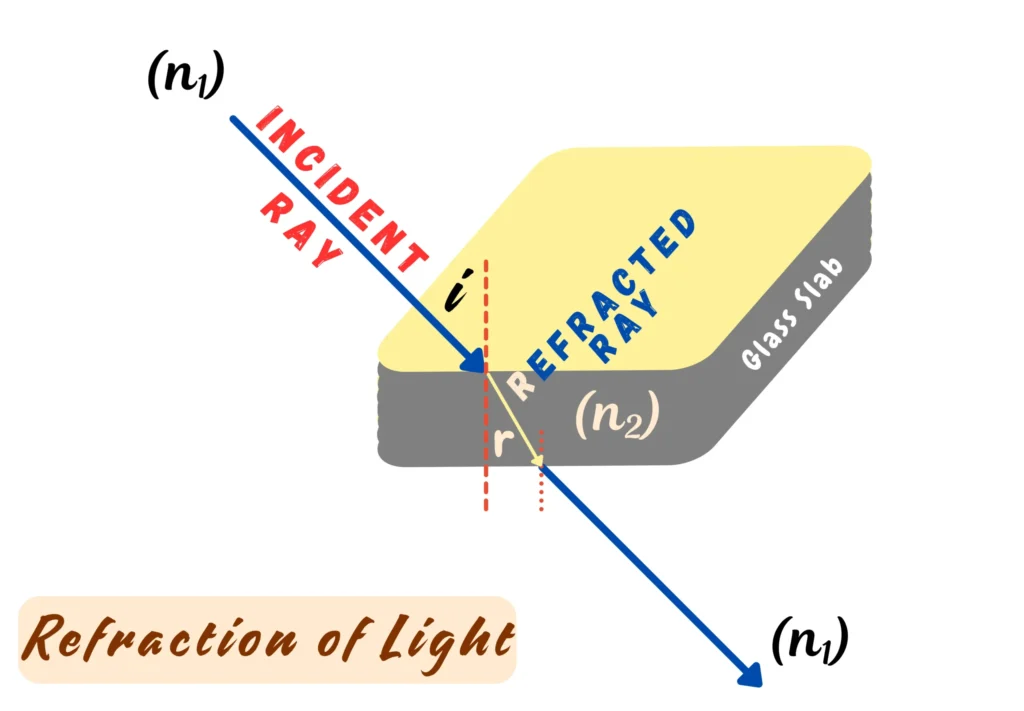
Refraction is the bending of a light ray when it passes from one medium into another, for instance; from air into water or glass.
Unlike reflection (where light returns to the original medium), refracted light continues into the new medium but in a different direction (or angle).
Why Does It Happens?
Refraction happens because light travels at different speeds in different materials. In vacuum or air light moves fastest; in glass, water, or diamond it moves more slowly.
When a wavefront of light enters a medium at an angle, one side of the wave slows before the other, and the change in speed produces a change in direction resulting in the path bending.
Refractive Index
The refractive index ![]() is a ratio of speed of light in a vacuum to the speed of light in a medium.
is a ratio of speed of light in a vacuum to the speed of light in a medium.
Mathematical Formulation
![]()
Where:
 = speed of light in vacuum
= speed of light in vacuum = speed in the medium
= speed in the medium- = refractive index
Refrative index tells you how much slower light is in a medium compared to vacuum. The value of ![]() for different media are given here:
for different media are given here:
| Media | Refractive Index |
| Air | 1.0003 |
| Water | 1.33 |
| Diamond | 2.42 |
| Ordinary Glass | 1.5 |
Qualitative Consequences
- If light enters from a rarer medium to a denser medium, it slows down and bends toward the normal.
- If light enters from a denser medium to a rarer medium, it speeds up and bends away from the normal.
Laws of Refraction (Snell’s Law)
Refraction is governed quantitatively by Snell’s Law. The law states that:
“The ratio of the sines of the angles of incidence and refraction equals the inverse ratio of the speeds (or equivalently the ratio of refractive indices) of the two media”.
According to this law:
- The incident ray, the refracted ray, and the normal all lie in the same plane.
- The ratio of sine of the angle of incidence ‘i’ to the sine of the angel of refraction ‘r’ is always equal to a constant ‘n’.
Mathematical Formulation
According to the statement:
![]()
![]()
![]()
![]()
Where:
 = speed of light in vacuum
= speed of light in vacuum = speed of light in the medium 1 and medium 2
= speed of light in the medium 1 and medium 2 = refractive indices of medium 1 and medium 2
= refractive indices of medium 1 and medium 2 = angle between the incident ray and the normal in medium 1
= angle between the incident ray and the normal in medium 1 = angle between the refracted ray and the normal in medium 2
= angle between the refracted ray and the normal in medium 2
![]()
Alternatively, it can also be written as:
![]()
Simple Experiments
- Pencil in water: Immerse a pencil partly in a glass of water. From the side, the pencil appears bent at the water surface because the light from the submerged part refracts at the water–air boundary before reaching your eye.
- Mirage on a hot road: On hot surfaces, air right above the ground is much warmer (and less dense) than air higher up. This gradient in refractive index bends light from the sky toward the road, making the road look reflective — often seen as distant “pools” of water.
- Lenses (glasses, cameras): Lenses are pieces of glass or plastic shaped to refract light in controlled ways, focusing or spreading rays to form images. This is how eyeglasses correct vision, and how cameras focus light onto film or a sensor.
- Rainbows: Sunlight refracts and disperses in water droplets — different wavelengths (colours) bend by slightly different amounts — producing the spectrum we see in a rainbow.
- Fibre optics: Light is kept inside thin glass fibres by total internal reflection and can travel long distances with very low loss — the basis for modern internet cables.
Total Internal Reflection
If light tries to go from a denser to a rarer medium and the angle of incidence is large enough, refraction cannot occur and all light reflects back internally. This is called total internal reflection.
Total internal reflection happens when the incident angle exceeds a material-specific critical angle.
Critical Angle
Critical angle can be defined as:
“The minimum angle of incidence in a denser medium at which light is refracted along the boundary (i.e., the angle of refraction is 90°) when passing into a rarer medium”.
Mathematical Expression
If light travels from medium 1 to medium 2, it can be given as:
For general case:
For denser-to-air transition:
Where,
- C = critical angle
 = refractive indices of medium 1 and medium 2
= refractive indices of medium 1 and medium 2
The principle of total internal reflection is the backbone of the fibre optics.
Historical Note
One of the most important early figures in optical science was Ibn al-Haytham (aka Alhazen), a great scholar from Islamic Golden Age.
In his Kitāb al-Manāẓir (Book of Optics), he conducted systematic experiments and used experimental evidences and geometry to support his theories. He carefully studied reflection, refraction, and image formation. His experimental approach laid foundations for the scientific method.
Fast-forward to modern times: the same principles of reflection and refraction led to inventions such as:
- Camera
- Telescope
- Microscope
- Fibre-Optic Communications
What began as geometric rules about angles now powers global information networks.
Why Do Colours Separate? | The Dispersion of White Light
The white light consists of different colours (wavelengths). Each colour of light travel at slightly different speed in the same medium, so according to Snell’s Law they refract by different amounts. The red colour bends the least and violet the most.

Dispersion of light explains many colour phenomena in nature and technology. For instance:
- sparkle of diamonds
- chromatic aberration (colour fringing) in lenses
Modern Connections and Why This Matters
Understanding reflection and refraction exceeds beyond academics. It supports technologies that shape modern life.
- Imaging: Cameras, medical imaging devices, and scientific instruments all rely on controlling reflection and refraction precisely.
- Telecommunications: Fibre optics depend on total internal reflection to route data accurately and efficiently.
- Sustainability and energy: Solar concentrators and reflectors use mirror geometry to target sunlight and improve energy capture.
- Everyday design: From eyewear to road safety signs, optics influence product design and safety.
Grasping these two behaviours also builds intuition for other wave phenomena (sound, water waves).
Conclusion
Reflection and refraction are two simple yet elegant responses of light. When light meets the boundary of a surface, it either bounce back or bend through.
Where this leads next?
Understanding these ideas clears the path to the next big topics:
- Optical Instruments
- Lenses & Mirrors
- Image Formation
- Microscopes
- Telescope
- Our Sight
Frequently Asked Questions (FAQs)
Write the major differences between reflection of light and refraction of light.
| Reflection | Refraction |
| Light bounces back into the same medium. | Light bends and passes into another medium. |
| Occurs on smooth, shiny surfaces like mirrors. | Occurs at the boundary between two transparent media. |
| Angle of incidence = angle of reflection. | Follows Snell’s law ((n_1 \sin i = n_2 \sin r)). |
The critical angle for a beam of light passing from water into air is 48.8 degrees. What does happen to the light rays with an angle of incidence greater than this angle?
If the angle of incidence is greater than 48.8°, no refraction occurs. The light is totally reflected back into the water — this is total internal reflection.
What do you understand by reflection of light? Draw a diagram to illustrate reflection at a plane surface.
Reflection of light is the bouncing back of light rays from a polished surface, such as a mirror, into the same medium.
Diagram

Where i = angle of incidence, r = angle of reflection.
State laws of reflection. Describe how they can be verified graphically. Also describe the following terms used in reflection: (i) normal (ii) angle of incidence (iii) angle of reflection
Laws of Reflection
- The angle of incidence equals the angle of reflection.
- The incident ray, reflected ray, and normal all lie in the same plane.
Verification (Graphically)
By measuring the angles of incidence and reflection using a protractor and mirror — plotting them gives a straight line showing equality.
Terms
- Normal: Perpendicular line at the point of incidence.
- Angle of incidence (i): Between incident ray and normal.
- Angle of reflection (r): Between reflected ray and normal.
Define refraction of light. Describe the passage of light through parallel-sided transparent material. Which of the quantity (or quantities) does not changed during refraction of light?
Refraction is the bending of light when it passes from one transparent medium to another due to a change in speed.
Parallel-Sided Glass Slab
Light bends toward the normal when entering and away from the normal when leaving — the emergent ray is parallel to the incident ray.
Unchanged Quantities
- Frequency and colour remain the same.
- Speed and wavelength change.
Define the following terms used in refraction: (i) angle of incidence (ii) angle of refraction
- Angle of incidence (i): Between the incident ray and the normal in the first medium.
- Angle of refraction (r): Between the refracted ray and the normal in the second medium.
What is meant by refractive index of a material? How would you determine the refractive index of a rectangular glass slab? On which factors the index of refraction depend?
The refractive index (n) of a material is the ratio of the speed of light in vacuum to that in the material.
![]()
Determination (Glass Slab)
By measuring angles of incidence and refraction using pins and applying Snell’s law.
Dependency
- Nature (density) of medium
- Wavelength of light
- Temperature
State the laws of refraction of light and show how they may be verified using rectangular glass slab and pins.
Laws of Refraction
- The incident ray, refracted ray, and normal all lie in the same plane.
- The ratio
 is constant for a given pair of media — Snell’s law.
is constant for a given pair of media — Snell’s law.
Verification
Use a rectangular glass slab and pins to trace incident and emergent rays; measure angles i and r, and verify the ratio ![]() is constant.
is constant.
What is meant by the term total internal reflection? State the conditions for total internal reflection.
When light travels from a denser medium to a rarer medium and hits the boundary at an angle greater than the critical angle, it is completely reflected back into the denser medium. This is referred to as total internal reflection.
Conditions for Total Internal Reflection
- Light travels from denser to rarer medium.
- Angle of incidence > critical angle.
What is critical angle? Derive a relationship between the critical angle and the refractive index of a substance.
The minimum angle of incidence in the denser medium for which the angle of refraction is 90°.
Relation with Refractive Index
For general case: ![]()
For denser-to-air transition: ![]()
Where,
- C = critical angle
 = refractive indices of medium 1 and medium 2
= refractive indices of medium 1 and medium 2
What are optical fibres? Describe how total internal reflection is used in light propagating through optical fibres.
Thin, flexible strands of glass or plastic that transmit light signals using total internal reflection.
Working
Light entering one end of the fibre strikes the inner walls at angles greater than the critical angle, so it reflects internally along the fibre until it exits at the other end — even through bends.

