Well, a journey through the realm of rounding off to significant figures can show us the path, “how to express our measurements accurately?” Here we shall learn about these two concept and try to understand why they matter.
Table of Contents
Introduction
Have you ever wondered why science teacher emphasises the importance of being accurate in measurements? Whether we are measuring liquids in a lab or calculating distances or sizes in physics, precision is crucial!
Similarly, in our daily lives, we frequently encounter situations where precision is crucial. For instance, when cooking a recipe that calls for 3.8 teaspoons of salt, adding 4 teaspoons may seem feasible. However, this small difference in quantity can result in a dish that is more salty.
These examples highlight the importance of understanding how to manage numbers—not just for students and professionals but for everyone.
Rounding Off to Significant Figures
Two fundamental concepts that help us handle numbers are round off and significant figures. Rounding off simplifies numbers, while significant figures indicate how precise those numbers are.
Accuracy of Physical Quantities | What Affects It?
Tools for Measurement
The tools we use for measurement can affect accuracy. A ruler with millimetre markings (such as Vernier calipers) is more precise than one with just centimetre markings (like a meter ruler).
Observer Skill Level or Measuring Technique
An observer should always measure consistently and correctly. For instance, if we are measuring the height of a plant, we need to make sure that we look at the measuring tape from eye level to avoid mistakes.
Number of Observation
Even the best tools in our hand can lead to mistakes if we are not careful. So, take multiple readings to make sure we are getting it right.
Measurement Techniques
In everyday life and science, we often encounter numerical values that are too long or complicated. To make sense of these numbers, we use various techniques such as estimation, rounding off, and significant figures.
With these methods, we can simplify our calculations and improve communication about measurements. Here, we shall see two out of the three mentioned techniques i.e., the rounding off and significant figures in the context of physical quantities.
Rounding Off
Rounding off can be defined as:
“The process of approaching a number to a desired place value by reducing the number of significant.”
Why We Round Off
Sometimes, we deal with long numbers that can be hard to read. However, rounding off helps us to simplify these numbers while keeping them close to the original value.
Rounding is an approximation technique used to reduce the number of digits in a number while keeping its value close to the original. In this process, the digits in a number are rounded off to a certain place value which means they are either raised a stage or remain the same.
Rules for Rounding Off
The simplification of a number via rounding off helps to communicate measurements clearly. Below are some key rules and examples for rounding.
Identify the Digit to Round
The first step is to determine the digit to which we need to round a number, whether to the nearest 10, 100, 1000, or a specific decimal place (dp) such as 1 dp, 2 dp, etc.
Apply the Rounding Rule
Once the digit to round is finalised, follow the following chart either to round up (raised a stage) or round down (remain the same) the number.
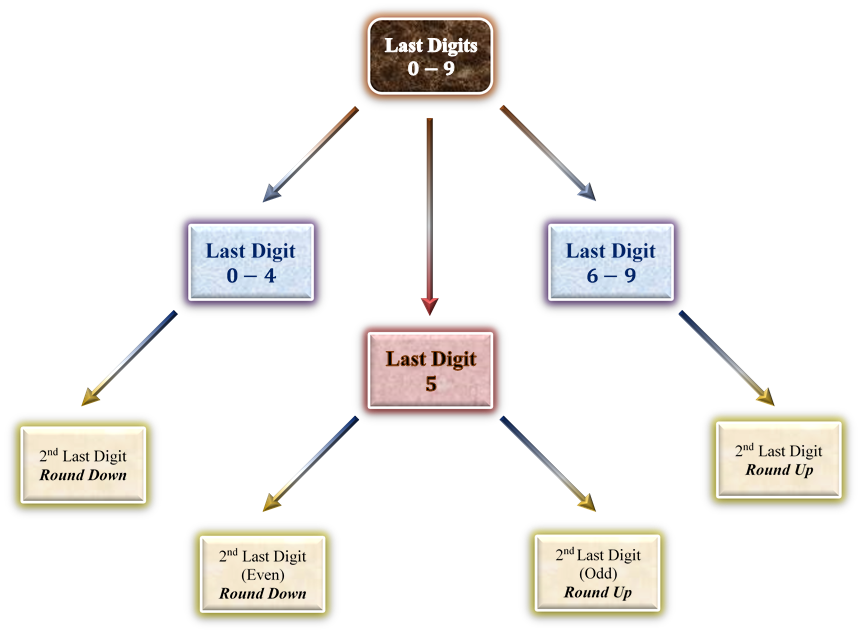
Note that, for integers (numbers containing negative values), we need to round off the numbers to the closest 10.
Rounding Off to Decimal Places
Rounding can also be applied to decimal places (dp):
- Upto 1 dp: 3.76 rounds to 3.8, while 3.24 rounds to 3.2.
- Upto 2 dp: 5.678 rounds to 5.68, while 5.432 rounds to 5.43.
- Upto 3 dp: 2.3456 rounds to 2.346, while 2.3443 rounds to 2.344.
Rounding Off to the Nearest 10, 100, and 1000
Rounding can be applied to a stated place value, for instance:
- Nearest 10: 47 rounds to 50, while 43 rounds to 40.
- Nearest 100: 234 rounds to 200, but 267 rounds to 300.
- Nearest 1000: 1543 rounds to 2000, while 847 rounds to 1000.
What are significant figures?
Significant figures are the digits in a number that reflect precision of a measured value. They start from the first non-zero digit. These figures not only help indicate the precision of a measurement but also provide the confidence in the data being presented.
Define Significant Figures
They are defined as,
“all the known digits plus one estimated or doubtful digit in a measured quantity.”
They are also known (and found in literature) as significant digits, sig figs, or simply s.f.
Why Significant Figures Matter
Significant figures are the digits in a number that contribute to its precision. They indicate the reliability of a measurement. Using the correct number of significant figures helps convey how precise a measurement is.
Significant Figures and Accuracy of a Measurement
Precision of measurement depends upon the number of significant digits. For instance, a better instrument yields more number of significant and hence, gives a more precise measurement. On the contrary, a poor instrument gives less number of significant digits and hence less precision.
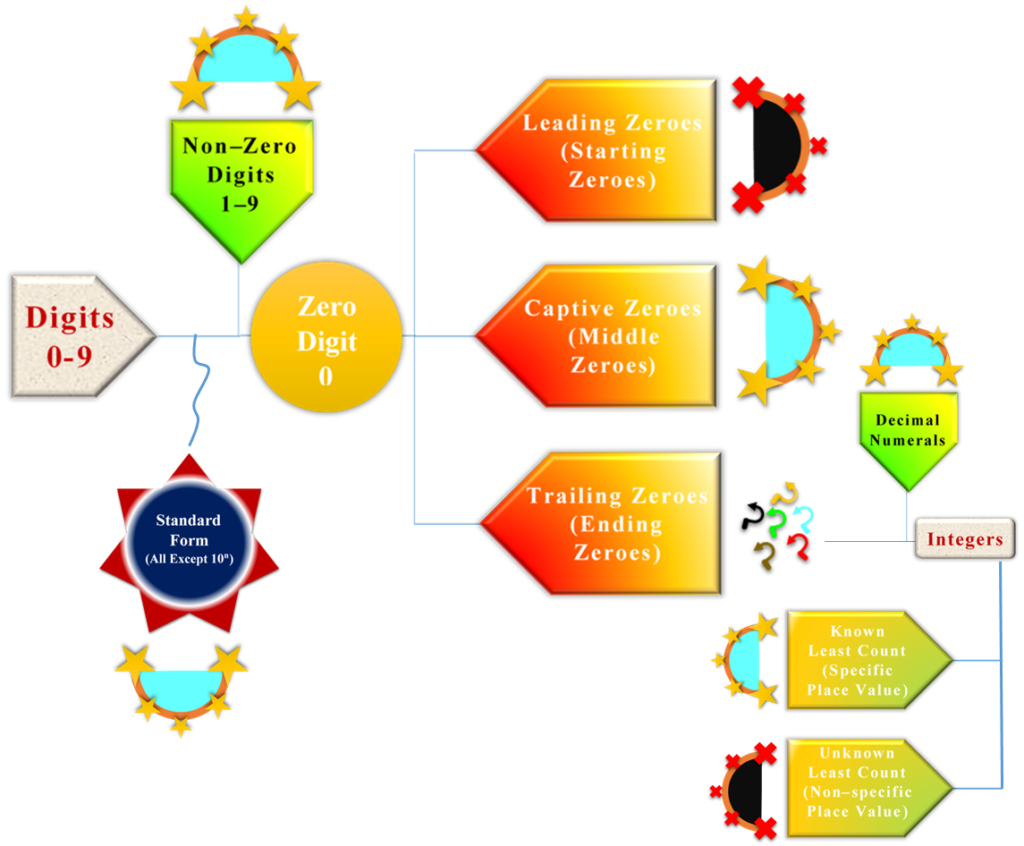
Rules for Determining Significant Figures
Sig figs rules with examples are discussed below. Here, the starred arcs are sig figs and cross arcs are non–significant.
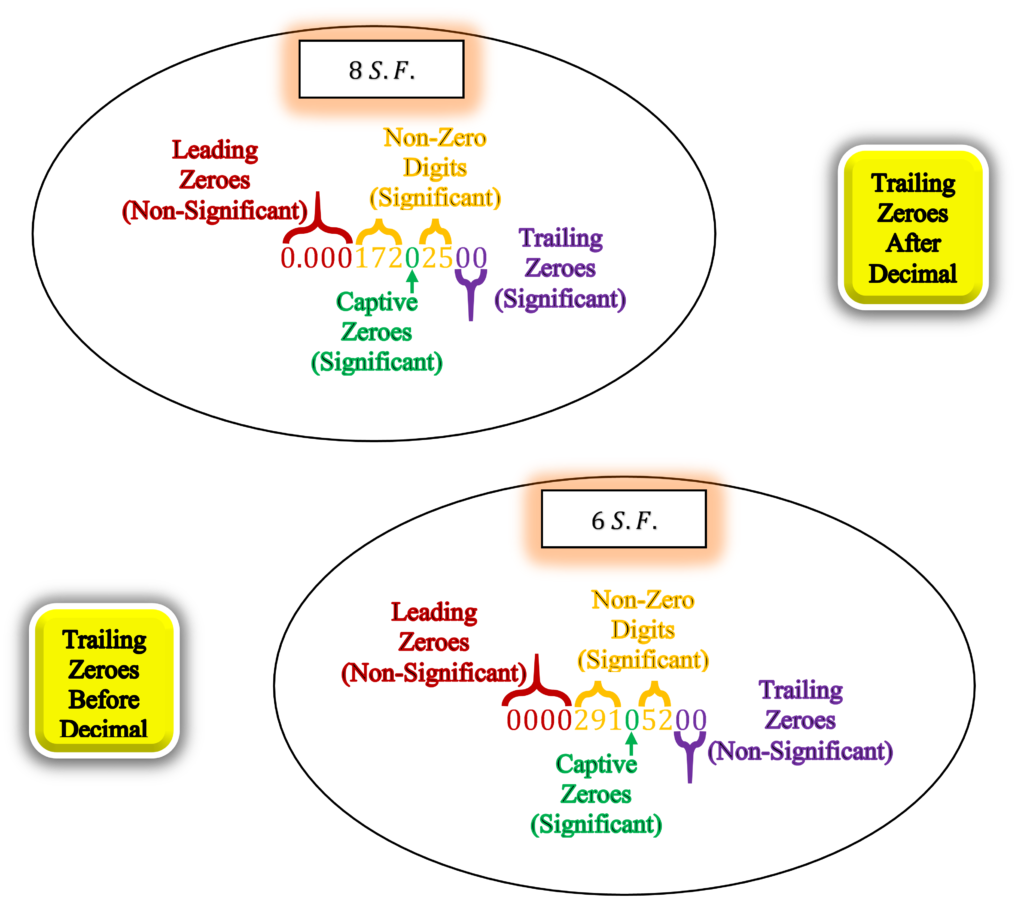
Example
The examples (in the figure) below show how to determine significant digits.
The Role of Significant Figures
Precision
Sig figs reflect the precision of measurements. For example, 12.30 has four significant digits, while 12.3 has three.
Calculations
When performing calculations involving integers, decimal numeral, and/or scientific notation, the final result must have the same number of significant digits as the measurement with the least precision (or least number of significant digits) or to the stated place value.
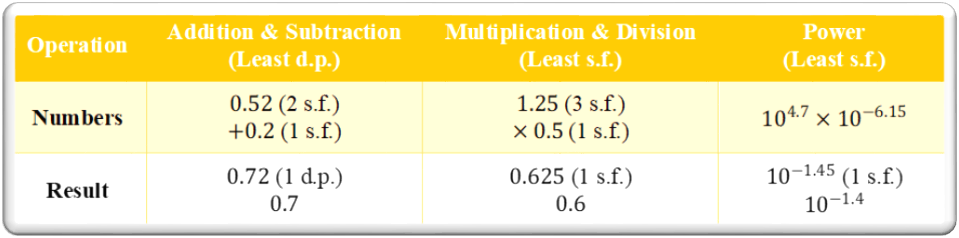
Communicating Uncertainty
They help scientists and engineers communicate the uncertainty inherent in measurements. A higher number of significant digits indicates greater certainty.
Conclusion
Rounding and sig figs are essential techniques in dealing with physical quantities. They not only simplify our numerical expressions but also enhance the clarity and reliability of scientific communication.
These techniques allow us to make informed decisions based on measurements, ensuring accuracy and precision in our work.
In summary, rounding is a helpful tool for simplifying numbers, while sig figs provide insight into the accuracy of those numbers. Both are approximation techniques that aid in conveying essential information clearly and effectively.
Frequently Asked Questions (FAQs)
What is rounding off in mathematics and physics?
Rounding is the process of simplifying a number to a desired place value, such as to the nearest 10, 100, or decimal places. It helps make long numbers easier to work with while maintaining their approximate value.
How do you round off numbers to the nearest decimal places?
To round a number to stated decimal places, identify the place value you want to round to (e.g., 1 or 2 decimal places) and follow the rule: if the digit immediately after your place value is 5 or higher, round up; if it is lower than 5, round down.
What are significant figures and why are they important?
Significant digits are the digits in a number that reflect its precision. They are essential in scientific measurements to indicate the precision and reliability of data.
How do you determine significant figures in a number?
Significant digits start from the first non-zero digit. Every non-zero digit is significant, and zeros can be significant depending on their position (e.g., captive zeros are significant, while leading zeros are not).
What are the rules for rounding off numbers in physics?
To round numbers in physics, follow these steps: identify the place value to which you need to round, then apply the rounding rule. If the digit after the rounding place is 5 or more, increase the rounding place by 1; if less than 5, leave it unchanged.
How do you use significant figures in scientific calculations?
When performing scientific calculations, the result must have the same number of significant digits as the number in the calculation with the fewest significant figures. This ensures the precision of the final result matches the least precise measurement.
Why do scientists use significant figures in measurements?
Scientists use significant digits to indicate the precision of their measurements. This helps communicate the level of certainty and accuracy in their data, which is critical for reliable scientific results.
How do trailing zeros affect significant figures in a decimal number?
Trailing zeros in a decimal number are significant. For example, in 2.50, the trailing zero is significant because it indicates precision to two decimal places.
Can significant figures be used in both large and small numbers?
Yes, sig figs apply to both large and small numbers. In scientific notation, all digits are significant except for the exponent (10n), which helps manage very large or small values.
What is the difference between rounding off and significant figures in physics?
The former simplifies a number to a specific place value, while the latter reflect the precision of a measurement. Both are used in scientific communication but serve different purposes—one for simplicity, the other for accuracy.
