The 3 types of motion i.e., vibratory motion, oscillatory motion, and simple harmonic motion (SHM) are key types of movement studied in detail due to their significance in both natural and engineered systems.
Table of Contents
Introduction
Motion and its types is a fundamental concept in physics. It describes how objects move and interact under the influence various forces. There are different types of motion in physics. Among them, the 3 back and forth type of motions are of great interest for engineering purpose.
Vibratory Motion, Oscillatory Motion, and Simple Harmonic Motion
The three motions sometimes are used interchangeably as well. Here, we shall see what these types of motions are and how they differ from each other.
1. Vibratory Motion
“Vibratory motion refers to the rapid, repetitive movement of an object around a fixed position.”
In such motion, particles move back and forth about a mean position within a small range.
Example
- The vibration of a guitar string when plucked.
- A mobile phone vibrating on a flat surface.
2. Oscillatory Motion
“Any motion where an object repeatedly moves back and forth around an equilibrium position is called oscillatory motion.”
It is a broader term. While vibratory motion is typically high-frequency and small-scale, oscillatory motion can occur at various speeds and amplitudes.
Key Features
- Requires a restoring force (like gravity or elasticity).
- Occurs around a mean position.
Example
- The swinging of a pendulum.
- The oscillation of a spring-mass system.
3. Simple Harmonic Motion (SHM)
Simple Harmonic Motion is a specific type of oscillatory motion where the restoring force acting on the object is directly proportional to the displacement from its equilibrium position and acts in the opposite direction.
Mathematical Formulation
Mathematically, the restoring force F is given by:
Here,
- F: Restoring force
- k: Force constant (spring constant in case of springs)
- x: Displacement from equilibrium position
SHM is described by sinusoidal functions, making it predictable and periodic in nature.
Features of SHM
Some important features of SHM are listed here.
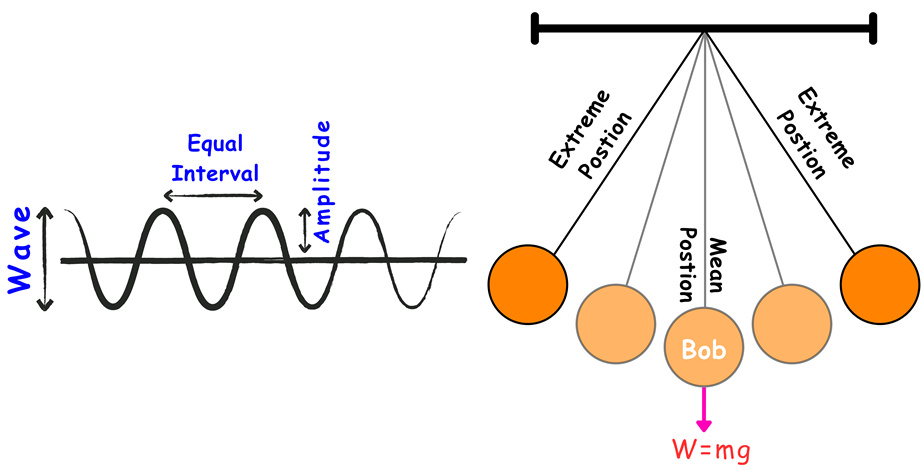
Periodic Motion
SHM repeats itself in equal intervals of time about its mean position.
Restoring Force and Acceleration
The force and acceleration are proportional to displacement and directed toward the equilibrium.
Magnitude of Acceleration
At the mean position, the acceleration is zero, whereas, at extreme position, acceleration is maximum.
Magnitude of Velocity
At mean position, the velocity is maximum, and, at extreme position, it is zero.
Energy Conservation
Total energy remains constant and shifts between kinetic (at mean position) and potential (at extreme position) forms.
Sinusoidal Nature
Displacement, velocity, and acceleration in SHM can be expressed as sine or cosine functions.
Examples of SHM
1. Ball and Bowl System
In this system, when a ball placed inside a bowl is displaced, it oscillates back and forth about the lowest point of the bowl.
The curvature of the bowl ensures the restoring force is proportional to displacement, leading to SHM.
Energy Changes
The energy changes in a ball and bowl system are as follows:
Extreme Positions
At maximum displacement (extreme position or edges of the bowl), the ball has maximum potential energy and zero kinetic energy.
Mean Position
At the equilibrium position (mean position or bottom of the bowl), the ball has maximum kinetic energy and minimum potential energy.
Total Energy During Motion
The total energy remains constant throughout the motion.
2. Motion of a Simple Pendulum
A pendulum is a classic example of SHM, provided the amplitude of oscillation is small.
The bob swings back and forth around its equilibrium position due to the restoring force provided by gravity.
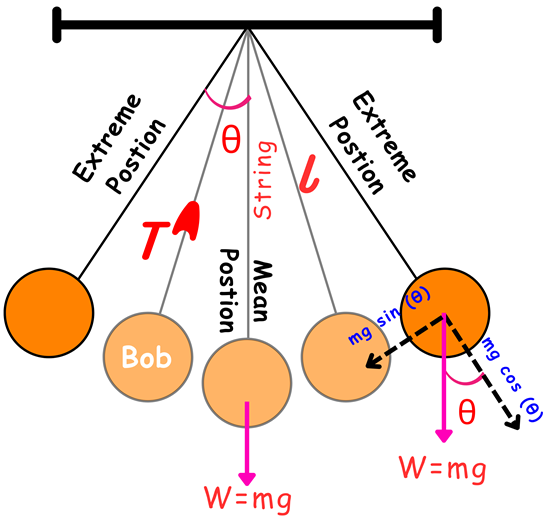
Force Analysis
In the absence of air drag, a simple pendulum experiences forces as tension and weight.
Tension (T)
This force passes through the sting and is directed from the bob to the support.
Weight (W)
This force is directed towards the ground and is dependent upon the mass of the bob.
Net Force
The next force vary from mean position to extreme postion.
Mean Position
At mean position, the net force is zero, because, 
.
Extreme Positions
At extreme positions, the net force is non-zero, because,
However, 
is the effective component of force and is directed towards the mean position.
Energy Changes
The changes in energy of simple pendulum system are as follows:
Extreme Positions
At the highest points of the swing (extreme positions), the pendulum has maximum potential energy and zero kinetic energy.
Mean Position
At the lowest point of the swing (equilibrium), it has maximum kinetic energy and minimum potential energy.
Total Energy During Motion
During the motion of a simple pendulum, the total energy remains conserved.
Time Period (T)
For a pendulum, it is a time required to move form one extreme to other extreme and back. It is given by;
Here,
- T = Time Period
- l = Length of string
- g = gravitational acceleration
Terms that Characterise SHM
Amplitude (A)
The maximum displacement of the object from its equilibrium position is called amplitude.
Period (T)
The time taken to complete one full oscillation is called time period or simply period.
Frequency (f)
The number of oscillations per unit time, measured in Hertz (Hz) is called frequency.
Angular Frequency (
)
The rate of change of the phase of motion, measured in radians per second, is called angular frequency.
Phase
It describes the state of motion at a particular time and is crucial in comparing SHM systems.
Conclusion
Vibratory, oscillatory, and SHM are interconnected, with SHM being a specific type of oscillatory motion governed by a linear restoring force.
Examples of ball and bowl and the pendulum help illustrate the principles of SHM, especially energy transformation between kinetic and potential forms.
Understanding these concepts is essential as they form the basis for more complex physical systems, from the design of mechanical clocks to the analysis of molecular vibrations in chemistry.
Frequently Asked Questions (FAQs)
What is vibratory motion, and how is it different from oscillatory motion?
The former refers to rapid, repetitive back-and-forth movement around a fixed position, often at high frequency and small range, such as the vibration of a guitar string.
Whereas, the later is a broader term, encompassing all repetitive movements around an equilibrium position, including slower, larger-scale motions like the swinging of a pendulum.
Is simple harmonic motion (SHM) a type of oscillatory motion?
Yes, SHM is a specific type of oscillatory motion where the restoring force is directly proportional to the displacement from equilibrium and acts in the opposite direction.
What are some real-life examples of SHM?
Examples of SHM include the oscillation of a simple pendulum, the movement of a mass on a spring, and the motion of a ball in a bowl when displaced.
What is the mathematical formula for the restoring force in SHM?
The restoring force in SHM is given by , where 
is the restoring force, 
is the spring constant, and 
is the displacement from the equilibrium position.
How does energy change during SHM?
In SHM:
- At the mean position, kinetic energy is maximum, and potential energy is minimum.
- At extreme positions, potential energy is maximum, and kinetic energy is zero.
- The total energy of the system remains constant, shifting between kinetic and potential forms.
What are the key characteristics of SHM?
- SHM is periodic and sinusoidal in nature.
- The restoring force and acceleration are proportional to displacement and directed toward equilibrium.
- Velocity is maximum at the mean position and zero at extreme positions.
- Energy is conserved, alternating between kinetic and potential energy.
What is the difference between amplitude and period in SHM?
Amplitude (A): The maximum displacement of the object from its equilibrium position.
Period (T): The time taken to complete one full oscillation or cycle.
What is the formula for the time period of SHM in terms of angular frequency?
The time period is given by , where is the angular frequency.
How does a pendulum demonstrate SHM?
A pendulum exhibits SHM when the amplitude of its swing is small. The restoring force due to gravity is proportional to the displacement, and energy alternates between kinetic and potential as it oscillates around its equilibrium position.
What is the significance of studying SHM in engineering and science?
Understanding SHM is crucial for analysing and designing systems like mechanical clocks, suspension systems, and molecular vibrations in chemistry. It also serves as a foundation for studying waves and advanced oscillatory phenomena.