Understanding Floating Point representation in computing as well as IEEE 754 standards is essential to handle large and small values.

Introduction

In computing, floating-point notation enables the representation of a wide range of real numbers, including extremely large and small values. It breaks them into parts for more flexible storage and calculations.

Floating-point notation is a standard in scientific computing, graphics, and engineering due to its ability to handle fractional numbers and vast magnitudes.

Real Numbers

Real numbers include all values that can represent a quantity along a continuous line. This includes:

Whole numbers: 0, 1, 25, 100
Fractions/Decimals: 0.5, -3.14, 7.75
Very small or large values: 0.0001, 1.5 × 10⁹

Storing Real Values in a Computer Memory

Real numbers are essential in computing for representing:

Currency (e.g., $12.99)
Graphics (e.g., pixel brightness)
Measurements (e.g., temperature, speed)
Scientific simulations (e.g., atomic calculations)

Unlike integers, storing real values in computer memory accurately as binary is harder due to their infinite or repeating binary representation. This is where floating point come into play.

Floating-Point Notation

Floating-point notation represents real numbers in computers. This notation includes extremely large and small values.

Floating Point Format

Floating-point numbers are typically represented in the format:

$\text{(-1)}^s \times \text{mantissa} \times 2^{\text{exponent}}$

$s$ | $\text{mantissa}$ | $2^{\text{exponent}}$

Where:

s is the sign bit (0 = positive, 1 = negative)
Mantissa (or significand) holds the significant digits
Exponent shifts the decimal (or binary) point using a power of 2

Why Floating Point?

Floating-point representation allows computers to perform varied task. It is widely used in different walks of life.

Why Use Floating Point? | Functions and Applications

Conversion Steps

Step 1: Identify real and fractional part.

Step 2: Convert both parts into binary.

Step 3: Write in the binary in the normalise form.

Step 4: Use IEEE 754 Representation standards and extract the sign bit, exponent, and mantissa based on the chosen bit format.

Floating Point Conversion Steps - IEEE 754 Representation Standards

Commonly Used Standards bit formats for Floating Point (IEEE 754 Standard)

Computers follow the IEEE 754 standard for floating-point representation. Two primary formats of this standard are:

a. Single Precision (32-bit)

Component	Bits	Purpose
Sign	1	0 = positive, 1 = negative
Exponent	8	Encodes the power of 2 (bias = 127)
Mantissa	23	Stores significant digits

b. Double Precision (64-bit)

Component	Bits	Purpose
Sign	1	0 = positive, 1 = negative
Exponent	11	Bias = 1023
Mantissa	52	More precision than 32-bit

Example

Convert 6.022 × 10²³ to 32-bit and 64-bit IEEE 754.

Step 1: Identification of real and fractional part (real part = 6, fractional part = .022)

Step 2: Write the standard number to binary approximation (shown in the figure).

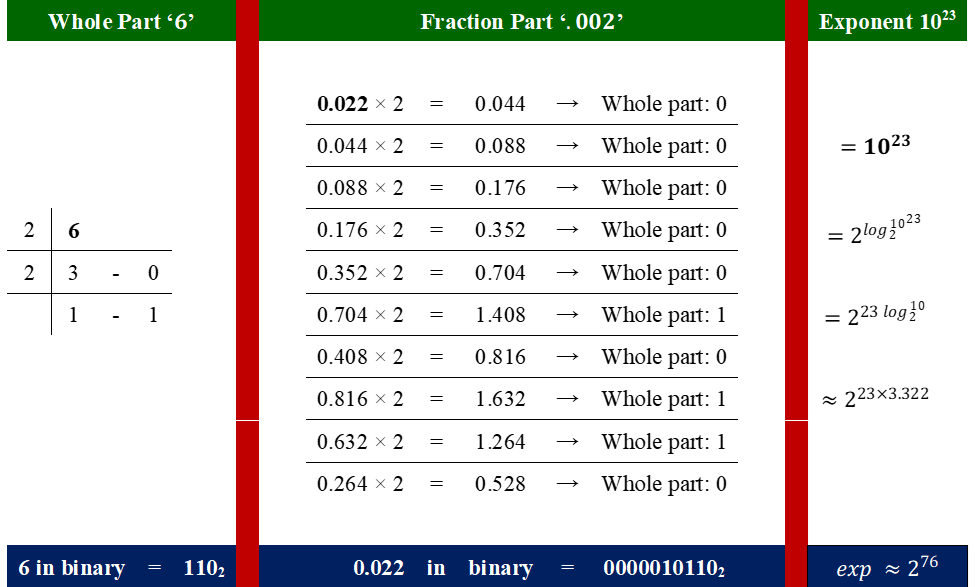
Real Number to Floating Point - Understanding Floating Point Representation in Computing

The final form of the binary is as follows:

6.022 ≈ 110.0000010110₂

Exponent 10²³ ≈ 2^76.406

6.022 × 10²³ ≈ 110.0000010110₂ × 2^76.406

Step 3: Writing the number in normalised form provides:

6.022 × 10²³ ≈ 110.0000010110₂ × 2^76.406

6.022 × 10²³ ≈ 1.100000010110₂ × 2² × 2^76.406

6.022 × 10²³ ≈ 1.100000010110₂ × 2⁷⁹

Step 4: Extract components (sign bit, exponent, and mantissa):

Using two different IEEE 754 formats, the binary equivalent of the floating-point notation is:

6.022 × 10²³ ≈ 1.100000010110₂ × 2⁷⁹ (Normalised binary)

a. Single Precision (32-bit)

According to IEEE 754 32-bit format:

Component	Bits
Sign	1
Exponent	8
Mantissa	23

s = 0 (Number is positive)
Exponent = 79 + 127 (bias) = 206 = 11001110₂
Mantissa = 100000010110 (drop leading 1, bits after the binary point) = 10000001011000000000000 (padded to 23 bits)

Final Representation

Final 32-bit = S | Exponent | Mantissa

Final 32-bit = 0 | 11001110 | 10000001011000000000000

b. Double Precision (64-bit)

According to IEEE 754 64-bit format:

Component	Bits
Sign	1
Exponent	11
Mantissa	52

s = 0 (Number is positive)
Exponent = 79 + 1023 (bias) = 1102 = 10001001110₂
Mantissa = 100000010110 (drop leading 1, bits after the binary point) = 1000000101100000000000000000000000000000000000000000 (padded to 52 bits)

Final Representation

Final 32-bit = S | Exponent | Mantissa

Final 64-bit = 0 | 10001001110 | 1000000101100000000000000000000000000000000000000000

Floating-Point Accuracy and Errors

Common issues in floating points that causes inaccuracies are as follows:

Rounding Errors (limited bits force approximations)
Overflow/Underflow (exponent too large or small to represent)
Loss of Significance (subtracting nearly equal values can wipe out precision)

Example

For a number 0.1 in decimal system, the binary equivalent is:

0.1 (decimal) = 0.000110011001100…₂ (binary)

This shows 0.1 cannot be represented precisely in binary using a finite number of bits. Similarly,

0.1 + 0.1 + 0.1 + … (10 times) $\neq$ 1.0

0.1 + 0.1 + 0.1 + … (10 times) = 0.9999999… (actual case, tiny rounding error)

These rounding errors can:

Accumulate in loops
Cause bugs in finance or physics simulations
Lead to loss of precision

Be aware of rounding errors and precision limitations.

Key Information to Remember

It is advised to keep these crucial information in mind about IEEE 754 Floating-Point Formats.

Component	Single Precision (32-bit)	Double Precision (64-bit)
Total Bits	32 bits	64 bits
Sign Bit	1 bit	1 bit
Exponent Bits	8 bits	11 bits
Mantissa Bits	23 bits	52 bits
Exponent Bias	127	1023
Exponent Range (Unbiased)	−126 to +127	−1022 to +1023
Smallest Positive Normalised Value	≈ 1.18 × 10⁻³⁸	≈ 2.23 × 10⁻³⁰⁸
Largest Positive Value	≈ 3.4 × 10³⁸	≈ 1.8 × 10³⁰⁸
Smallest Positive De-normalised Value	≈ 1.4 × 10⁻⁴⁵	≈ 4.9 × 10⁻³²⁴
Precision (decimal digits)	~7 digits	~15–17 digits

Why not 4, 8, or 16 bit?

4-bit & 8-bit are too small to hold meaningful floating-point data. It is not capable of even small-scale computation.

16-bit can store small real numbers but has too limited a range and insufficient precision for most scientific or real-world numeric tasks.

For big numbers like representing 6.022 × 10²³ (Avogadro’s number), only 32-bit or 64-bit formats are feasible.

Conclusion

Floating-point notation revolutionised computing by enabling the representation of data (real numbers) across extensive ranges. Though it has limitations, particularly with rounding errors, its advantages in precision and scalability make it indispensable for advanced computing.

Frequently Asked Question (FAQs)

What is floating point representation in computing?

Floating-point notation is a way to represent real numbers in computing, including very large and very small values. This notation divides the number into three parts: the sign, the mantissa (which contains the significant digits), and the exponent (which scales the value by a power of 2).

How does the IEEE 754 standard work in floating-point notation?

IEEE 754 is the standard for floating-point arithmetic in computers. It defines how floating-point numbers should be represented, with two main formats: single precision (32 bits) and double precision (64 bits).

Each format includes specific bit allocations for the sign, exponent, and mantissa to ensure consistency across systems.

What is the difference between single and double precision?

Single precision uses 32 bits: 1 bit for the sign, 8 bits for the exponent, and 23 bits for the mantissa. Double precision uses 64 bits: 1 bit for the sign, 11 bits for the exponent, and 52 bits for the mantissa. Double precision allows for a larger range and higher precision compared to single precision.

In the single precision, how many bits are used for the exponent?

(a) 23 bits
(b) 8 bits
(c) 11 bits
(d) 52 bits

In single precision (IEEE 754), the exponent is represented using 8 bits.

What is the approximate range of values for single-precision floating-point numbers?

(a) 1.4 × 10⁻⁴⁵ to 3.4 × 10³⁸
(b) 1.4 × 10⁻³⁸ to 3.4 × 10⁴⁵
(c) 4.9 × 10⁻³²⁴ to 1.8 × 10³⁰⁸
(d) 4.9 × 10⁻³⁰⁸ to 1.8 × 10³²⁴

(a) 1.4 × 10⁻⁴⁵ to 3.4 × 10³⁸

This is the approximate range of representable values for IEEE 754 single-precision format, including both normalised and de-normalised numbers.

How is the range of floating-point numbers calculated for single precision and double precision?

Feature	Single Precision (32-bit)	Double Precision (64-bit)
Sign Bit	1 bit	1 bit
Exponent Bits	8 bits	11 bits
Exponent Bias	127	1023
Exponent Range (raw)	1 to 254 (excluding 0 and 255 for special use)	1 to 2046 (excluding 0 and 2047 for special use)
Actual Exponent Range	–126 to +127	–1022 to +1023
Mantissa Bits	23 bits	52 bits
Smallest Positive Normalised	$2^{-126} \approx 1.18 \times 10^{-38}$	$2^{-1022} \approx 2.23 \times 10^{-308}$
Largest Positive Normalised	$2^{127} \times (2 - 2^{-23}) \approx 3.4 \times 10^{38}$	$2^{1023} \times (2 - 2^{-52}) \approx 1.8 \times 10^{308}$
Smallest Positive De-normalised	$2^{-149} \approx 1.4 \times 10^{-45}$	$2^{-1074} \approx 4.9 \times 10^{-324}$

Why is it important to understand the limitations of floating-point representation in scientific computing?

Understanding the limitations of floating-point is essential because:

Precision is limited: Some decimal values (like 0.1) cannot be represented exactly in binary.
Rounding errors occur: Repeated operations can accumulate tiny inaccuracies.
Incorrect results in sensitive calculations: Small errors can grow in simulations or numerical methods.
Debugging is harder: Errors may not be obvious and could cause subtle bugs.

What is the difference between normalised number and de-normalised number?

Feature	Normalised Number	De-normalised Number
Leading digit	Always 1 (implicit)	Can be 0 (no implicit 1)
Exponent bits	Not all 0s	All 0s (not representing zero)
Range	Wider, more accurate	Very close to 0
Precision	Higher (uses full mantissa bits)	Lower (some bits lost for leading zeros)
Purpose	Regular floating-point values	To avoid underflow, keep gradual precision near zero

Understanding Floating Point Representation in Computing | Storing Real Values in Computer Memory | 101 Comprehensive Guide

Table of Contents

Introduction

Real Numbers

Storing Real Values in a Computer Memory

Floating-Point Notation