Understanding the fundamentals of SHM and the mass-spring system is essential for ensuring the efficiency and functionality of various real-life systems.

Introduction

Oscillations are all around us, from the swinging of a pendulum to the vibrations of a guitar string. At the core of these motions is Simple Harmonic Motion (SHM).

Understanding SHM and the mass spring system is essential, they are fundamental to mechanical vibrations that can affect the efficiency of many engineering systems. This concept requires attention in both higher education and industry.

What is Simple Harmonic Motion (SHM)?

Simple Harmonic Motion is a type of motion where an object oscillates back and forth around an equilibrium position.

Features of SHM

For a body under consideration that is in SHM:

• The restoring force acting is directly proportional to its displacement (validating Hook’s Law).
• The force always acts toward the equilibrium position (ensuring a periodic and oscillatory motion).

SHM and the Mass-Spring System

Both SHM and the mass-spring system are the opposite sides of the same coin. Understanding these two concepts would establish a stronger foundation in the future studies of vibrational analysis.

The Mass-Spring System

A setup consisting of a spring attached from one end to a fixed support and the other end with a mass on a frictionless surface is called a mass spring system.

It is an ideal example of SHM when the spring obeys Hooke’s Law.

Mathematical Formulation

Consider a mass spring system as shown.

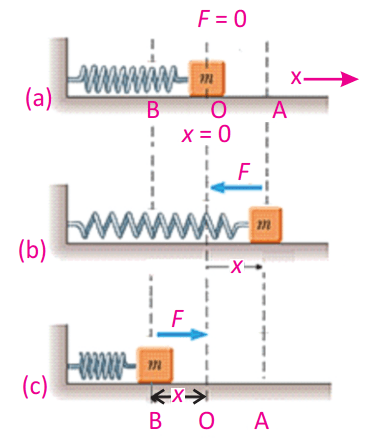
According to Hooke’s Law,

Here,

• F = restoring force
• x = displacement
• k = Spring Constant (Stiffness)

According to Newton’s Second Law of motion,

Equating two forces, we get,

Rearranging gives,

The constant k and m, given by , is equal to the square of and is shown below.

Here,

= angular frequency

The resulting equation of motion is given as,

Why the Negative Sign?

The negative sign in the equation indicates that the restoring force and resulting acceleration act in the opposite direction, pulling the system back toward equilibrium (mean position).

Without this opposing force, oscillations would not occur, and the system would just drift away.

What is Restoring Force?

The force responsible for pulling the system back to equilibrium is called the restoring force.

In a mass spring system, this force is proportional to the displacement () and acts as the key driver of oscillatory motion.

Force Analysis

The analysis of restoring force reveals the following things to us.

Mean Position ()

At mean position, we witness:

• The restoring force is zero because there is no displacement ().
• Speed is at its maximum, as the mass zips past equilibrium.
• Acceleration is zero since there is no force acting.

Extreme Positions ()

• The restoring force is maximum, trying to pull the mass back to equilibrium ().
• Speed is zero because the mass momentarily pauses to change direction.
• Acceleration is maximum because the force is strongest.

Energy Changes

In SHM, energy changes from potential to kinetic forms while keeping the total energy constant.

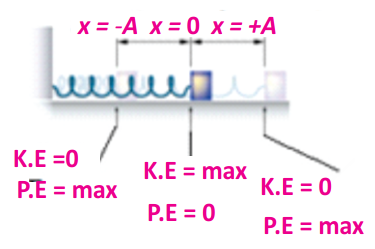
Mean Position

The transformation of energy at the mean position is as follows:

• Kinetic energy () is maximum because the mass is moving fastest.
• Potential energy () is zero since the spring is neither stretched nor compressed.

Extreme Positions

The energy at two extremes is as follows:

• drops to zero as the mass comes to a halt.
• is maximum because the spring is either fully compressed or stretched.

Total Energy at a Point

The total energy E of the system at any moment is given by:

This equation highlights that the energy of the system depends on the spring constant and the amplitude of oscillation, but not on time or position.

Time Period of a Mass-Spring System

The time taken by a mass spring system to complete one full oscillation is known as the time period (T).

For a mass spring system, this is given by,

This formula tells us that heavier masses (m) take longer to oscillate, while stiffer springs (higher k) lead to quicker oscillations. The time period of a mass spring system is independent of the amplitude, or the length of the spring.

Conclusion

The mass spring system is a key concept in understanding mechanical vibrations, a crucial aspect of engineering. Without this knowledge, many systems and equipment would not function optimally.

In short, SHM shows how nature seeks equilibrium. Hence, by studying it, we gain valuable insight into motion and system performance.

Frequently Asked Questions (FAQs)

What is Simple Harmonic Motion (SHM)?

SHM is a type of oscillatory motion where an object moves back and forth around a central equilibrium position. The motion is characterized by a restoring force proportional to the displacement from the equilibrium position.

How does a mass spring system demonstrate SHM?

A mass spring system demonstrates SHM when the spring obeys Hooke’s Law, which states that the restoring force is directly proportional to the displacement of the mass from its equilibrium position.

What is Hooke’s Law?

Hooke’s Law describes the restoring force in the spring, stating that it is proportional to the displacement: , where k is the spring constant and x is the displacement from the equilibrium position.

What is the role of the restoring force in SHM?

This force acts in the opposite direction to the displacement, pulling the object back towards the equilibrium position. This force is key to the oscillatory motion in SHM.

What is the mathematical equation for SHM in a mass spring system?

The equation of motion for SHM in a mass spring system is , where a is the acceleration, is the angular frequency, and x is the displacement from the equilibrium.

How do you calculate the time period of a mass spring system?

For a mass spring system, it is given by the formula , where m is the mass and k is the spring constant.

This indicates that heavier masses lead to longer oscillations, while stiffer springs result in faster oscillations.

What happens at the mean position in SHM?

At the mean position, the force (restoring) is zero, the speed of the mass is maximum, and the acceleration is zero since no force is acting at this point.

What happens at the extreme positions in SHM?

At the extreme positions, the restoring force is maximum, speed is zero, and the acceleration is also maximum as the object is about to change direction.

What is the total energy of a mass spring system?

The total energy E of a mass spring system is constant and is given by , where A is the amplitude.

The energy switches between kinetic and potential forms, but the total energy remains unchanged.

Why is the negative sign important in the equation for SHM?

The negative sign indicates that the force (restoring) always acts in the opposite direction to the displacement, ensuring that the object returns to its equilibrium position and continues oscillating. Without this force, the system would not oscillate.