To know about “what is a set in mathematics?” is beneficial and compulsory to advance in higher concepts like relations, functions, probability, and logic.

Introduction

In mathematics, the concept of sets is fundamental. Sets are used to group objects, numbers, or symbols that share a common property. In real life, you often hear about words like tea set, ice cream set, set of books, etc. All these cases refer to the collection of things.

In mathematics, the same idea applies —meaning a set is simply a collection of objects. Here, you will explore what sets are, how they are written, and the various types of sets that exist.

What is a Set?

A set can be defined as:

“A collection of well-defined and distinct objects.”

Here are 3 important things to notice:

Collection: Objects can be grouped.
Well-defined: There should be no ambiguity about what and who belongs to the set.
Distinct: All elements must be unique — no repetition is allowed.

Elements of a Set

The objects in a set are called elements of a set. They are also known as members or entries of a set. The elements of a set can be:

numbers
alphabets
mathematical or Greek symbols

Symbol of Element

The symbol $\in$ is used to show that an element belongs to a set.

Example

If $a$ is an element of set $A$ , you can write it as $a \in A$ .

How to Write a Set?

Here are the conventions for writing sets:

Set names are represented by capital letters (e.g., A, B, C, …).
Elements are written as lowercase letters, numbers, or symbols, separated by commas, and enclosed in curly brackets {}.
The order of elements does not matter.
Repetition is not allowed.

Example

$A = \text{Set of vowels} = \{a, e, i, o, u\}$

Validity Check

Set	Description	Is it a Set?
A = {a, e, i, o, u}	Well-defined and distinct	Yes
B = {e, l, e, p, h, a, n, t}	Well-defined but not distinct	No
C = {top mathematicians}	Collection but not well-defined	No
D = Set of fire	Not a collection	No

3 Methods to Represent a Set

Mainly, there are 3 methods to express a set.

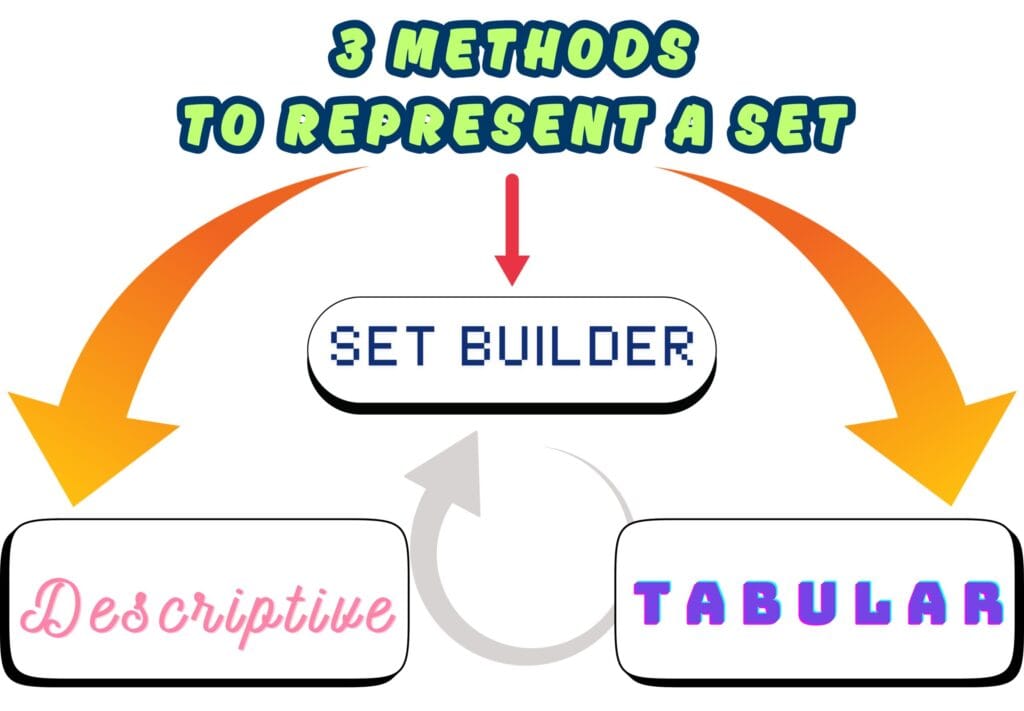
1. Descriptive Method

The descriptive method is a way to express a set of words or a sentence.

Example

A = Set of first five natural numbers
B = Set of rainbow colour names

2. Tabular Method (Roster Method)

It is also known as the “Roster Method” or “Listing Method” and represents elements explicitly within curly brackets.

Example

$A = \{1, 2, 3, 4, 5\}$
$B = \{\text{Violet, Indigo, Blue, Green, Yellow, Orange, Red}\}$

3. Set Builder Notation

The method of representation uses mathematical symbols to define elements of a set.

Example

$A = \{x \mid x \in \mathbb{N} \wedge 1 \leq x \leq 5\}$
$B = \{x \mid x \text{ is colour of the rainbow}\}$

Trick about Set Builder Notation

A set builder notation has three segments to pay attention to.

i. Declaration (such as $x \mid$ )

ii. Statement (such as $x \in \mathbb{N} \text{ or } x \text{ is colour of the rainbow}$ )

iii. Condition (such as $1 \leq x \leq 5$ )

Note:

The sign $\wedge$ – read as ‘and’ – separates the statement from the condition.
The condition may or may not be present in the set builder notation.

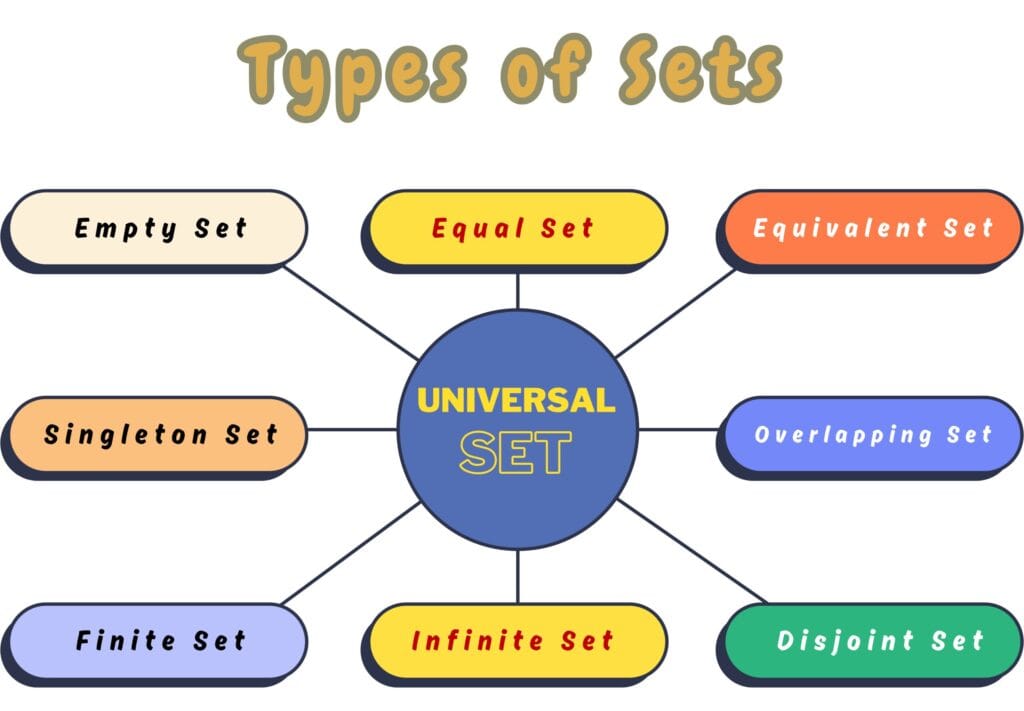
Types of Sets

The most common types of sets are given here.

Empty Set vs Singleton Set

Empty Set (Null Set)	Singleton Set
It is a set with no elements. It is denoted by $\phi$ or $\{\}$	A set with only one element.
For example: $A = \phi$	For example: $A = \{e\}$

Finite Set vs Infinite Set

Finite Set	Infinite Set
It is a set with countable elements.	A set with uncountable elements.
For example: $A= \text{Set of prime numbers below 100}$	For example: $A = \text{Set of all prime numbers}$

Disjoint Sets vs Overlapping Sets

Disjoint Sets	Overlapping Sets
Two sets that have no common elements.	Two sets with at least one common element.
For example: $A = \{0,2,4,6,8\}$ $B = \{1,3,5,7,9\}$ None of these elements are the same.	For example: $A = \{0,2,4\}$ $B = \{1,3,5,7,9\}$ $C = \{2,3,5\}$ Here, A & C and B & C are overlapping.

Equivalent Sets vs Equal Sets

Equivalent Sets	Equal Sets
Sets with the same number of elements (not necessarily the same elements). Equivalent sets are represented by $A \asymp B$	Sets with the same elements, possibly in a different order. The notation used for equal sets is $A = B$ .
For example: $A = \{a,e,i,o,u\}$ $B = \{0,2,4,6,8\}$ These are equivalent sets.	For example: $A = \{n,a,p\}$ $B = \{p,a,n\}$ Here, A & B are equal sets.

Universal Set

A set that contains all elements under consideration. It is the mother of all sets and is denoted by $U$ .

Example

$\mathbb{U} = \text{Set of real numbers}= \mathbb{R}$

Key Points to Remember

Types of elements are based on the number and arrangement of elements.
A universal set contains elements of all the sets under consideration.

Subsets

If all elements of set A are also in set B, then:

A is a subset of B
B is a superset of A

Representation of a Subset

It is represented by:

Subset: $A \subseteq B \text{or } A \subset B$
Superset: $B \supseteq A \text{or } B \supset A$

Note: The one facing the open end is the super set and the one facing the closed end is a subset.

Proper Subset

A subset that does not contain all elements of the parent set. It is denoted by the symbol $\subset$ .

Example

$A = \{a,b\}$
Proper subsets: $\phi, \{a\}, \{b\}$

Improper Subset

A subset that is identical to the original set. The notation used for the improper subset is $\subseteq$

Example

$A = \{a,b\}$
$\{a,b\} \subseteq A$

How to Write Subsets?

i. The first step is to count the elements.

ii. Secondly, write all possible combinations of the elements — including:

the empty set $\phi$
one-element subsets
two-element subsets
three and up to the full set

Some students find it harder to write the subsets and determine the proper and improper subsets. If you do, write in the comment section below and we shall guide you through.

Subset Facts

Total subsets = $2^n$
Proper subsets = $2^n - 1$
Every set has only one improper subset (itself)
Empty set has only one subset: $\phi$ (improper)
Singleton set has two subsets: $\phi$ (proper), and itself (improper)

Power Set

The power set of a set A is the set of all subsets of A. The notation used for the power set is $P(A)$ .

Example

The power set of $A = \{a,b\}$ is given below:

Subsets of A:

$\phi, \{a\}, \{b\}, \{a,b\}$

Power Set of A:

$P(A) = \{\phi, \{a\}, \{b\}, \{a,b\}\}$

Power Set Notes

$\phi \in P(A), \text{as well as, } \phi \subset P(A)$
$a \in A \text{ and } \{a\} \subset A, \text{but } a \notin P(A); \text{instead}, \{a\} \in P(A)$
Total subsets of a power set = $2^n$ , where $n$ is the number of elements in $A$ .

Conclusion

Understanding sets helps build the foundation for higher-level math topics like relations, functions, probability, and logic. These topics will be discussed in the subsequent post.

Topics — such as ‘sets’, types of sets, subsets, and power sets — are powerful tools in the field of mathematics. Once you grasp these concepts, you shall be better equipped to navigate the world of mathematics with confidence.

Frequently Asked Questions (FAQs)

What is a set in mathematics?

A set is a collection of well-defined and distinct objects, represented in curly brackets. For example:

$A = \{1, 2, 3\}$

How do you denote that an element belongs to a set?

We use the symbol $\in$ . For example:

$3 \in A \quad \text{means } 3 \text{ is an element of set } A$

What are the three methods to represent a set?

1. Descriptive Method

2. Tabular (Roster) Method

3. Set Builder Notation

What is the difference between a finite and infinite set?

A finite set has a countable number of elements.
An infinite set has uncountable elements.

For example:

$\text{Finite Set: } A = \{1, 2, 3, ..., 100\}$

$\text{Infinite Set: } \{1, 2, 3, ...\}$

What is a universal set?

A universal set contains all elements under discussion, denoted by $U$ . For example:

$U = \mathbb{R} \text{ (set of all real numbers)}$

What is a proper and an improper subset?

Proper subset: Excludes at least one element of the parent set. It is denoted by $\subset$ .
Improper subset: Includes all elements of the parent set. It is denoted by $\subseteq$ .

Example

$\{a\} \subset \{a, b\}, \quad \{a, b\} \subseteq \{a, b\}$

How many subsets does a set have?

If a set has $n$ elements, then:

$\text{Total subsets} = 2^n, \quad \text{Proper subsets} = 2^n - 1$

What is a power set?

The power set of $A$ , written as $P(A)$ , is the set of all subsets of $A$ .

Example

$A = \{a, b\}$

$P(A) = \{\phi, \{a\}, \{b\}, \{a,b\}\}$

Is the empty set a subset of every set?

Yes, the empty set $\phi$ is a subset of every set, including itself.

What is the difference between equal sets and equivalent sets?

Equivalent sets contain the same number of elements but not necessarily the same elements.
Equal sets contain the same elements and the order of elements does not matter.

$A = \{t,i,p\}$

$B = \{p,i,t\}$

$C = \{1,2,3\}$

Here, A & B are Equal Sets, but A & C and B & C are equivalent sets.

Table of Contents

Introduction

What is a Set?

Elements of a Set

Symbol of Element

Example

How to Write a Set?

Example

Validity Check

3 Methods to Represent a Set

1. Descriptive Method

Example

2. Tabular Method (Roster Method)

Example

3. Set Builder Notation

Example

Trick about Set Builder Notation

Types of Sets

Empty Set vs Singleton Set

Finite Set vs Infinite Set

Disjoint Sets vs Overlapping Sets

Equivalent Sets vs Equal Sets

Universal Set

Example

Key Points to Remember

Subsets

Representation of a Subset

Proper Subset

Improper Subset

How to Write Subsets?

Subset Facts

Power Set

Power Set Notes

Conclusion

Frequently Asked Questions (FAQs)

What is a set in mathematics?

How do you denote that an element belongs to a set?

What are the three methods to represent a set?

What is the difference between a finite and infinite set?

What is a universal set?

What is a proper and an improper subset?

How many subsets does a set have?

What is a power set?

Is the empty set a subset of every set?

What is the difference between equal sets and equivalent sets?

Leave a Comment Cancel Reply