Do you know, what is centripetal force? Well, it is a force that causes circular motion and is directed toward the centre of the circle.

Introduction

Circular motion is the movement of an object along a circular path. It is a common yet fascinating phenomenon in physics. When an object moves with constant speed in a circle, it is undergoing uniform circular motion.

In a circular motion, the speed of an object remains constant, however, it continuously changes its direction. This shows that there is a change in velocity at every instant, and hence, the acceleration.

But what causes this acceleration? The answer lies in the centripetal force. It is an inward force, and without it, the object would move off in a straight line due to inertia.

Centripetal Force

It is defined as,

“the net inward force acting on a body, causing it to change its motion from a linear path to a circular path at a constant (inward) acceleration.”

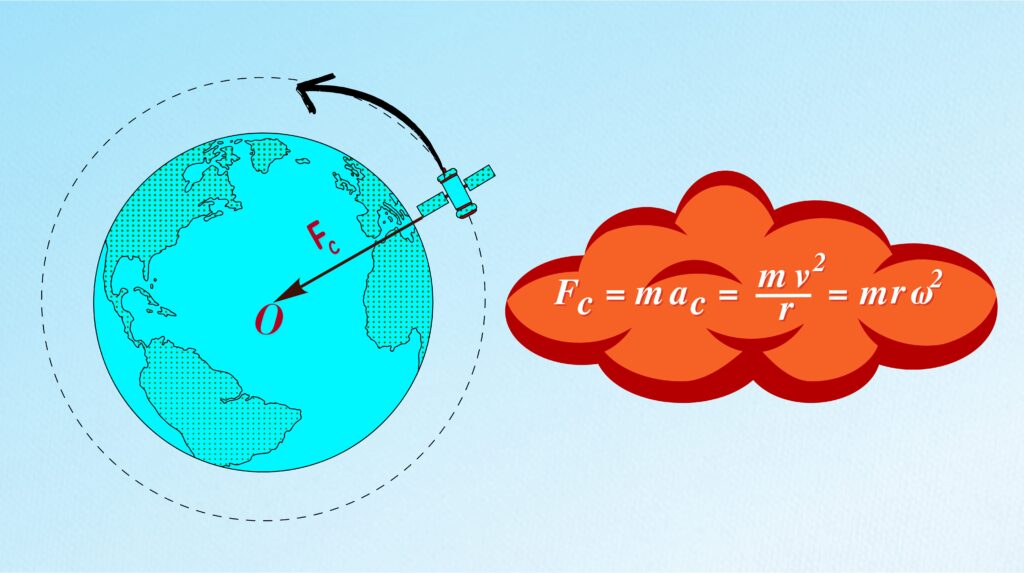
What is Centripetal Force - Orbiting Satellite

While its derivation often involves calculus, we shall take a visual and geometric approach in this guide to derive the formula and establish its connection between centripetal acceleration and force.

Mathematical Formulation

Consider an object moving with constant speed from point A to point B (as shown below), separated by a small angle $\Delta \theta$ , and having the different direction of velocity vectors at both A and B.

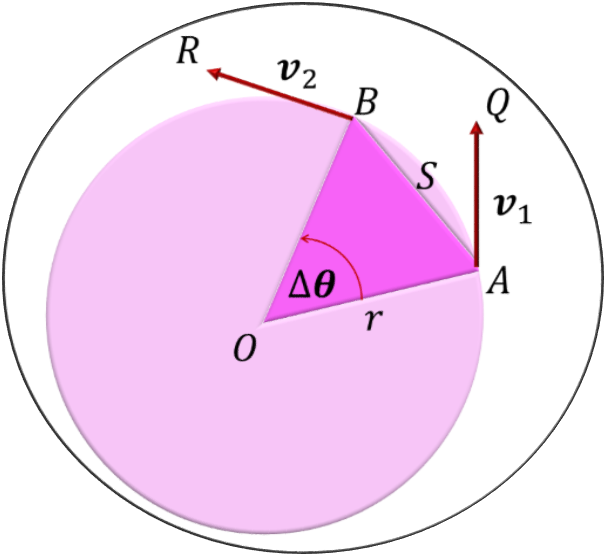
Circular Motion - Analysis for Centripetal Force and Acceleration

For the given case,

Velocity Vector at A = $\mathbf{v_1}$
Velocity Vector at B = $\mathbf{v_2}$
Change in Velocity = $\Delta \mathbf{v}$
Radius of the Circle = $r$
Distance between A & B = $S$
Angular Distance from A to B = $\Delta \theta$

Constructing the Triangles

Here, we have two triangles which are shown below.

Velocity Triangle PQR
Position Triangle AOB

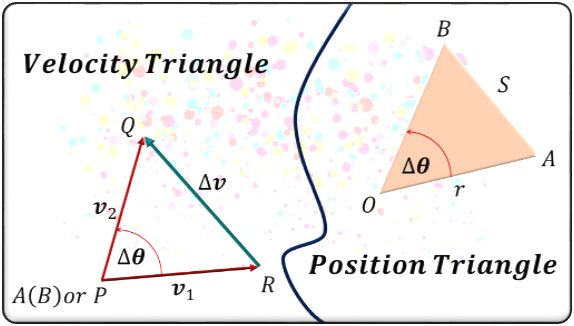
Position Triangle vs Velocity Triangle for a Circular Motion

Establishing Similarity

The two triangles (i.e., position triangle and velocity triangle) are similar. It is because the angle $\Delta \theta$ subtended at the center of the circle corresponds to the angle between the velocity vectors. Their relationship is represented as a proportion:

$\frac{\Delta v}{v} = \frac{S}{r}$

Approximating the Arc Length

For small angles ( $\Delta \theta \to 0$ ), we have:

$\overset{\frown}{AB} \approx \overline{AB}= S$

The straight-line distance $\overline{AB}= S$ is given by,

$S = v \Delta t$

Here, $\Delta t$ is the time taken to traverse a distance of $S$ from A to B.

Deriving the Equation

Substituting $S = v \Delta t$ into the proportion:

$\frac{\Delta v}{v} = \frac{v \Delta t}{r}$

$\Delta v = \frac{v^2 \Delta t}{r}$

$\frac{\Delta v}{\Delta t} = \frac{v^2}{r}$

$a = \frac{v^2}{r}$

$a_c = \frac{v^2}{r}$

$a_c =$ centripetal acceleration

Centripetal Acceleration

It is defined as,

“the instantaneous acceleration of an object, moving with uniform speed and directed towards the centre of the circle.”

Key Principles of $a_c$

This acceleration reveals two key principles.

$a_c \propto v^2$

$a_c \propto \frac{1}{r}$

These relationships show why tighter turns or higher speeds require more force to maintain circular motion.

Connecting Centripetal Acceleration to Force

From Newton’s 2^nd law of motion,

$F_c = ma_c$

Substituting $a_c = \frac{v^2}{r}$ ,

$F_c = \frac{mv^2}{r}$

Here,

$F_c =$ centripetal force

It is the inward force required to keep an object moving in a circle. It could be provided by tension, gravity, friction, or any other force depending on the situation.

Conclusion

Centripetal acceleration and force are essential for understanding circular motion in physics. From orbiting planets to designing racetracks and rides in amusement parks, understanding centripetal force plays a vital role.

To all those individuals to whom phenomena such as the orbiting planets, the tension in a spinning rope, or the friction of a car on a curved road fascinate, knowing the answer to the question, “What is centripetal force?” is important.

Now, we shall learn the practical scenarios where this force plays a crucial role, such as banking curves in roads, designing satellites in orbit, or analysing the physics of a roller coaster loop, etc.

Frequently Asked Questions (FAQs)

What is centripetal force?

It is the net inward force that causes an object to follow a circular path. It is directed toward the center of the circle.

What is the formula for centripetal force?

The formula is:

$F_c = \frac{mv^2}{r}$

Here,

$m$ = mass of object
$v$ = constant speed
$r$ = radius of the circle

What provides centripetal force in real-life scenarios?

Tension in a rope during a spinning motion
Gravitational force for planets in orbit
Friction between tires and the road for a turning car

What happens if centripetal force is removed?

Without this force, an object would move off in a straight line due to inertia.

What is centripetal acceleration?

It is the acceleration directed toward the center of a circular path, given by:

$a_c = \frac{v^2}{r}$

Does centripetal force depend on speed?

Yes, this force is proportional to the square of the speed and is given as,

$F_c \propto v^2$

What role does radius play in centripetal force?

This force is inversely proportional to the radius of the circle and is given as,

$F_c \propto \frac{1}{r}$

Is centripetal force a separate type of force?

No, it is not a separate force. It is the resultant force acting toward the center of the circular path, which could be tension, gravity, or friction.

How is the centripetal force used in designing roads?

Banking of roads ensures that a component of the normal force provides the necessary $F_c$ for safe turns.

What is the difference between centripetal and centrifugal forces?

The former is a force that acts toward the center of the circle, while the later is perceived as an outward force experienced in a rotating frame of reference.

What is Centripetal Force? | 101 A Comprehensive Visual Approach

Table of Contents