What is momentum in Physics? It is a fundamental concept in classical mechanics, acting as a bridge between theoretical concepts and practical applications.
Table of Contents
Introduction
Momentum is a fundamental concept in physics, intricately linked to motion, collisions, and conservation laws. It helps to explain a variety of physical phenomena, from collisions to explosions. It is the measure of the motion of an object.
It gives insight into how difficult it is to stop a moving object. It also provides insights into motion and energy transfer. The conversion of momentum helps us to solve everyday physics problems and complex engineering challenges.
Momentum
It is defined as,
“the product of mass and velocity is called momentum.”
Key Properties of Momentum
Some key properties of momentum are given below.
Representation
Momentum is typically denoted by the symbol ![]() .
.
Unit
In the SI system, momentum is measured in kilogram meters per second (kg·m/s) or newton-second (Ns).
Type of Quantity
Momentum is a derived quantity. It is composed of one base quantity (m) and one derived quantity (![]() ).
).
Nature of Quantity
It is a vector quantity as it requires both magnitude and direction.
Mathematical Formulation
Mathematically, it is represented by,
![]()
Here,
 Momentum
Momentum Mass
Mass Velcity
Velcity
What is momentum in Physics? | Physical Meaning
Momentum can be thought of as the “quantity of motion” an object possesses. In other words, it quantifies how difficult it is to stop a moving object. The larger the momentum, the greater the force required to bring it to rest and vice versa.
Think of a heavy truck and a small car moving at the same speed. The truck has much more momentum (quantity of motion) due to its larger mass, making it harder to stop.
Applications of Momentum
Momentum is crucial in understanding collisions, explosions, and various physical phenomena. There are numerous applications of momentum in our real life, spanning from sports, vehicle safety, and space exploration to many others.
Law of Conservation of Momentum
One of the most fundamental laws in physics is the Law of Conservation of Momentum, which states that,
“in an isolated system, the total momentum before an event (e.g., collision or explosion) is equal to the total momentum after the event.”
Isolated System
It is defined as,
“a system where no external forces act on the interacting objects is called an isolated system.”
Example
- The gas is enclosed in a well-insulated cylinder.
- Two ice skaters pushing off each other on frictionless ice.
Events Governed by Momentum Conservation
Momentum conservation is the key to understanding collisions and explosions.
1. Collisions
When two objects hit each other, irrespective of the way they hit, it is referred to as a collision.
Types of Collision
Momentum conservation plays a crucial role in collisions, which are classified into two types.
- Elastic Collision
- Inelastic Collision:
Elastic Collision
It is defined as,
“the collision in which both momentum and kinetic energy are conserved is called elastic collision.”
Example
Two billiard balls collide on a pool table.
Inelastic Collision
It is defined as,
“The collision in which momentum is conserved, but some kinetic energy is lost, is called inelastic collision.”
Example
A car crash where the vehicles stick together.
Mathematical Formulation
Consider two cars moving in the same direction as shown below. Here,

![]() mass of 1st car
mass of 1st car
![]() mass of 2nd car
mass of 2nd car
Before collision
Initially, both cars are moving at different speeds.
Speed of ![]()
Speed of ![]()
If ![]() , the cars will collide.
, the cars will collide.
After Collision
Both cars start to move at the same speed.
Mutual Speed of ![]()
According to the law of conservation of momentum,
Momentum Before Collision = Momentum After Collision
OR
Initial Momentum = Final Momentum
OR
Sum of momentum before Collision = Sum of Momentum after Collision
OR
![]()
For the given case of collision,
![]()
![]()
2. Explosions
An explosion occurs when an object breaks apart into multiple fragments. Momentum conservation applies as the system’s initial momentum is equal to the vector sum of the final momenta of all fragments.
Example
- A bullet fired from a gun.
- A firework burst in mid-air.
Mathematical Formulation
Consider a rocket being launched as shown below. Here,
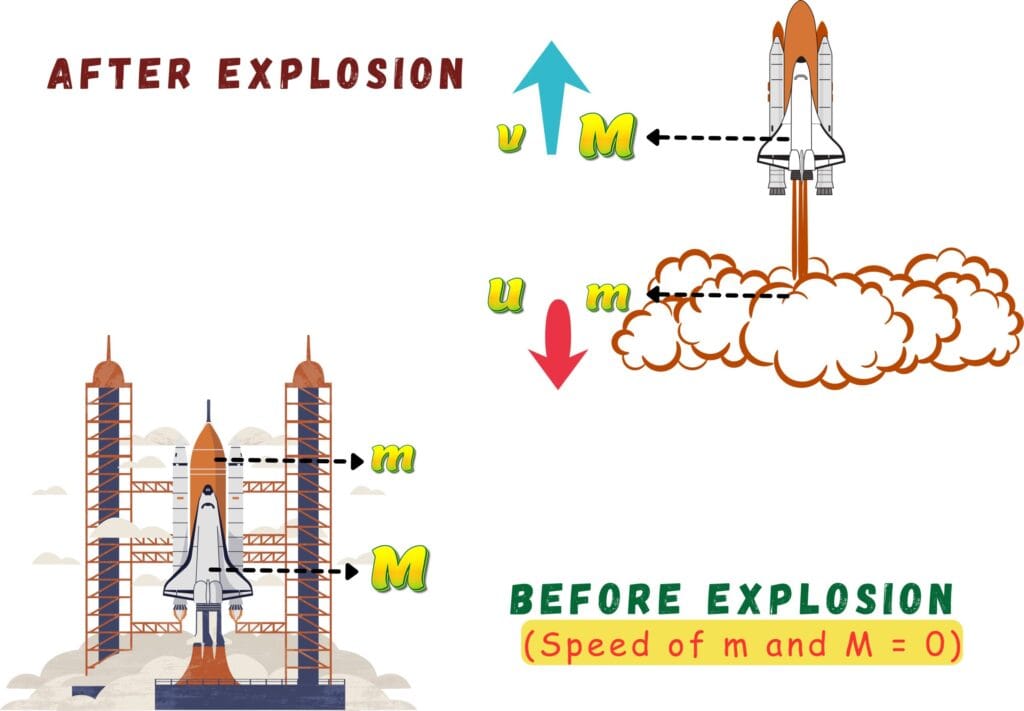
![]() mass of the rocket
mass of the rocket
![]() mass of the fuel exhaust
mass of the fuel exhaust
Before Explosion
Initially, the system (rocket + fuel) is stationary (at rest).
Speed of ![]()
Once the fuel starts to burn, the rocket accelerates.
After Explosion
Both rocket and fuel exhaust move at different speeds in opposite directions.
Speed of ![]()
Speed of ![]()
According to the law of conservation of momentum,
Momentum Before Collision = Momentum After Collision
OR
Initial Momentum = Final Momentum
OR
Sum of momentum before Collision = Sum of Momentum after Collision
OR
![]()
For the given case of explosion,
![]()
![]()
![]()
![]()
Why the Negative Sign?
The negative sign indicates that both the rocket and the fuel exhaust are moving in the opposite direction.
Conclusion
Momentum is a cornerstone of classical mechanics, bridging theoretical concepts with practical applications. From understanding collisions in daily life to enabling space missions, momentum plays a central role.
Whether analysing collisions or explosions, the principles of momentum are a vital tool for understanding the natural world. Understanding these events not only helps in theoretical physics but also finds practical applications in fields like engineering, ballistics, and astrophysics!
In a nutshell, it enables us to design better systems and solve real-world problems efficiently.
What are your thoughts on momentum? Share your experiences or questions in the comments below!
Frequently Asked Questions (FAQs)
What is Momentum in Physics?
Momentum is the product of an object’s mass and velocity, represented mathematically as ![]() .
.
Why is Momentum Important?
Momentum helps explain how objects move, collide, and transfer energy, making it a vital concept in physics and engineering.
Is Momentum a Vector Quantity?
Yes, momentum has both magnitude and direction, making it a vector quantity.
What are the Units of Momentum?
Momentum is measured in kilogram meter per second (kg·m/s) or newton-second (Ns).
What is the Law of Conservation of Momentum?
It states that in an isolated system, the total momentum before and after an event remains constant.
What is an Isolated System?
An isolated system is one where no external forces act on the objects within it.
What are Elastic and Inelastic Collisions?
Elastic Collision: Both momentum and kinetic energy are conserved.
Inelastic Collision: Momentum is conserved, but kinetic energy is not.
How is Momentum Conserved in Explosions?
In explosions, the initial momentum of the system equals the vector sum of the final momenta of all fragments.
What is an Example of Momentum Conservation?
Collision: Billiard balls hitting each other.
Explosion: A rocket launching into space.
Why is Momentum Important in Real Life?
Momentum principles are used in vehicle safety, sports, ballistics, and space exploration, making them crucial for solving practical and engineering problems.

