Do you know, what is torque in physics? Well, it is a fundamental concept in physics as well as in engineering that governs the rotational motion.

Introduction

Torque is the invisible force that can be seen in many places. For instance, the turning of a doorknob, the rotation of a wheel, or the functioning of sophisticated machinery are all utilising this key concept of physics.

In this blog, we shall explore the torque in-depth, discuss its properties, mathematical formulation, and applications in the real world.

Torque

Torque, also known as the turning effect of force, is defined as,

“the measure of the tendency of a force to rotate an object about an axis, fulcrum, or pivot.”

“the cross product of the moment arm ( $\mathbf{r}$ ) and the force ( $\mathbf{F}$ ) acting on a rigid body.”

“the product of the effective component of force and the position vector (moment arm), acting perpendicular to each other.”

$\text{Torque} = \text{Moment Arm} \times \text{Force}$

Key Terms Associated With Torque

From the above definitions, we witnessed torque as the rotational equivalent of force in linear motion and also observed the following terms.

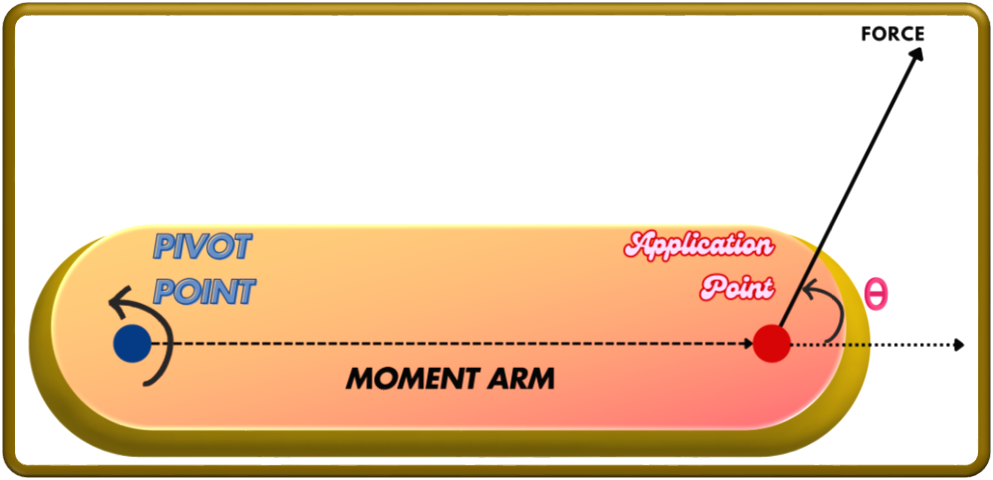
Pivot (or Axis of Rotation)

It is defined as,

“a fixed point, axis, or support around which an object rotates or is capable of rotating.”

It serves as the point of rotation or fulcrum in a system experiencing torque.

Force and the Pivot

If the force is acting at the pivot, there will be no torque as the point of rotation and point of application will coincide.

Moment Arm

It is defined as,

“the perpendicular distance from the axis of rotation to the line of action of the force.”

It is typically represented by the symbol ( $\mathbf{r} \text{or} \vec{r}$ ). It is the distance between the pivot point and the point of application of force (where the force is applied relative to the axis of rotation).

Force and the Moment Arm

If the force is acting parallel to the moment arm (passing through the pivot), there will be no torque as there will be no rotational effect.

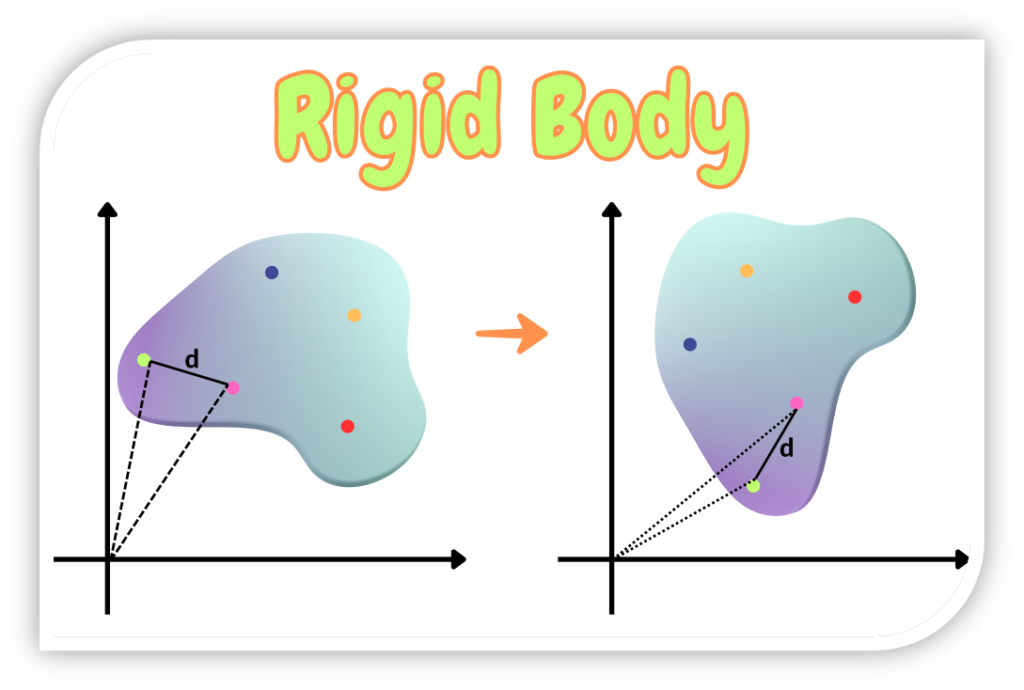
Rigid Body

It is defined as,

“an idealised solid object that does not deform under the influence of external forces and every point on it remains at a fixed distance relative to every other point.”

This assumption in the field of rotational dynamics simplifies the study of torque.

Key Properties of Torque

The key properties of torques are as follows:

Representation

Torque is represented by the symbol $\mathbf{tau} \text{or} \vec{\tau}$ .

Unit

The SI unit of torque is the Newton-meter (N\cdotm).

Type of Quantity

Torque is a derived quantity because it is the product of a derived (F) and a base (r) quantity.

Nature of Quantity

Torque is a vector quantity as it requires both magnitude and direction for its complete description.

Direction of Torque

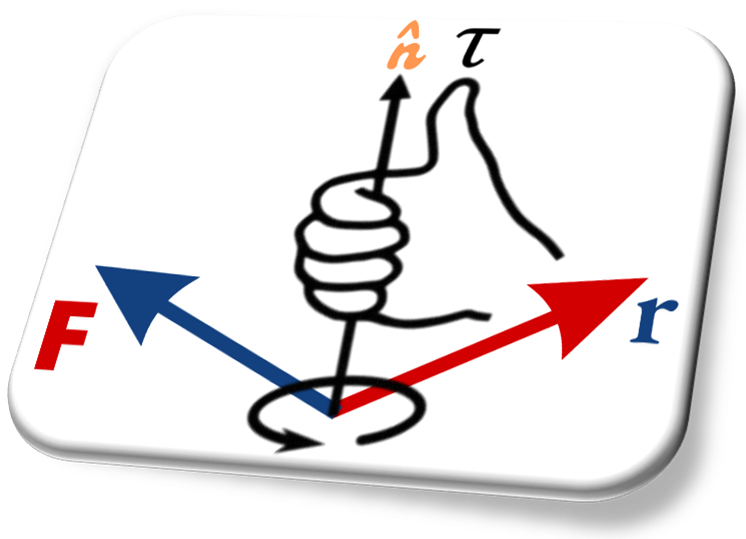
Its direction is perpendicular to both force and moment arm and is found by the right-hand rule.

Right-Hand Rule

This rule states that,

“place the right hand on the position vector and curl the fingers in the direction of the force vector, while subtending the smallest angle, the erected thumb will point in the direction of the torque vector, along an axis.”

Mathematical Formulation

Consider a rigid body subjected to a force inclined to the moment arm as shown below.

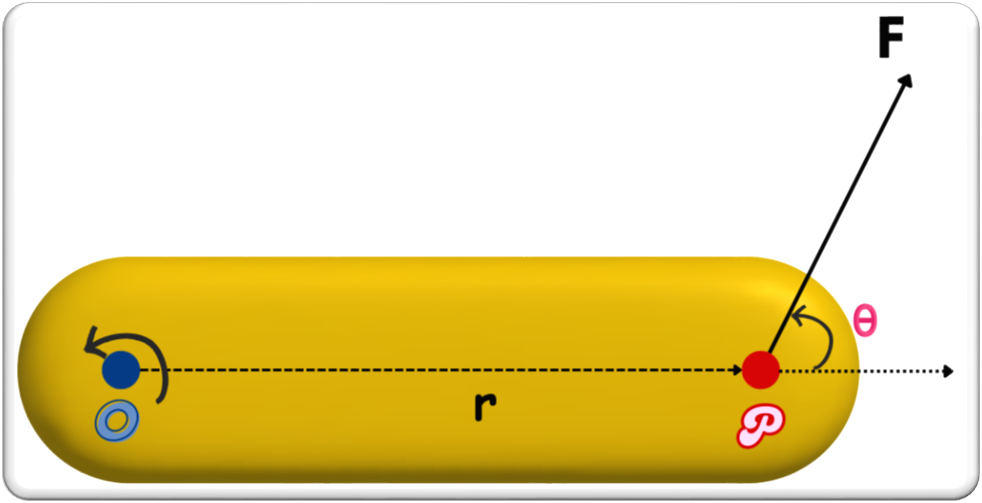
Here,

$r$ = moment arm
$F$ = applied force
$\theta$ = angle between the position vector (moment arm) and force vector

This shows that the magnitude of torque depends on the force, the distance from the axis, and the angle of application. The magnitude of torque can either be found by resolving the force into its components or resolving the moment arm into its respective components.

Determination of Torque by Resolving Force

As shown in the figure,

x-component of force = $F_x = F \cos\theta$
y-component of force = $F_y = F \sin\theta$

Considering the x-component,

$\tau = r \times F_x$

It is clear from the figure,

$F_x \parallel r$

Hence,

$\tau = 0$

Considering the y-component,

$\tau = r \times F_y$

It is clear from the figure,

$F_y \perp r$

Hence,

$\tau = r \times F \sin\theta$

Determination of Torque by Resolving Moment Arm

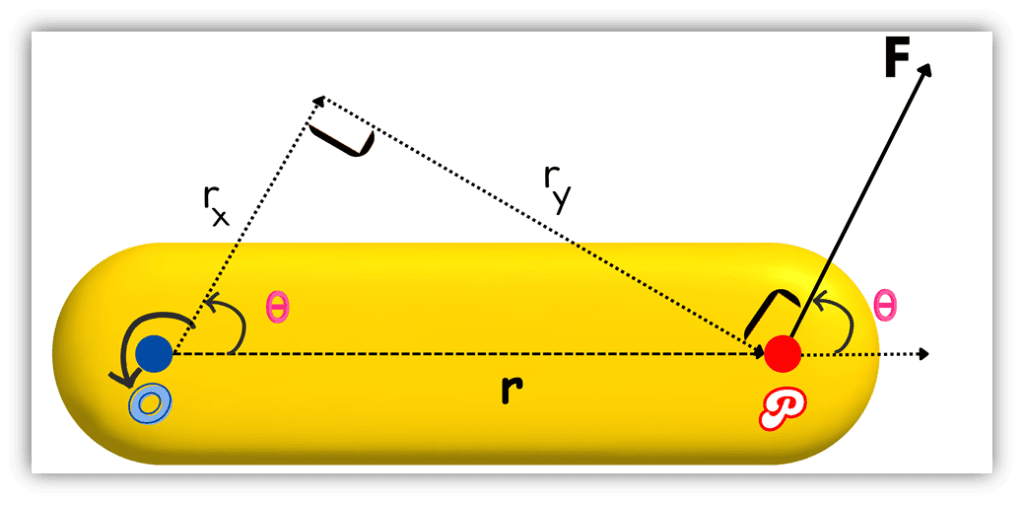
As shown in the figure,

x-component of force = $r_x = r \cos\theta$
y-component of force = $r_y = r \sin\theta$

Considering the x-component,

$\tau = r_x \times F$

It is clear from the figure,

$F \parallel r_x$

Hence,

$\tau = 0$

Considering the y-component,

$\tau = r_y \times F$

It is clear from the figure,

$F \perp r_y$

Hence,

$\tau = r \sin\theta \times F$

$\tau = r \times F \sin\theta$

Torque as a Cross-Product

$\vec{\tau} = \vec{r} \times \vec{F}$

$\mathbf{\tau} = \mathbf{r} \times \mathbf{F}$

$\mathbf{\tau} = (r F \sin\theta) \hat{\mathbf{n}}$

Magnitude of the Torque

To determine the magnitude of the torque, $r, F, and \theta$ are the deciding variables.

Maximum Torque

For maximum torque,

$r \neq 0$

$F \neq 0$

For the case of counter-clockwise torque,

$\sin\theta = 1$

We also know that from trigonometry,

$\sin\theta = [-1,+1], \where \theta = [\frac{-pi}/{2}, \frac{pi}/{2}]$

So, torque is maximum, if,

$\theta = \sin^{-1}(1)$

$\theta = 90^o$

$\theta = \frac{pi}/{2} \text{rad}$

For the case of clockwise torque,

$\sin\theta = -1$

Zero Torque

For zero or null torque,

Either,

$r = 0$

Or,

$F = 0$

Or,

$\sin\theta = 0$

$\theta = \sin^{-1}(0)$

$\theta = 0^o$

$\theta = 0 \text{rad}$

Torque vs. Force

Force initiates linear motion, whereas torque induces rotational motion.
Force results in the linear acceleration, while the torque results in the angular acceleration.
The force acts in a straight line, but torque is concerned with the rotational influence of an axis.

Torque vs. Moment

Torque and moment are closely related but contextually distinct.
Torque usually refers to a rotational effect (dynamic systems) due to a force, while moment often describes bending or twisting effects (static systems) within structural contexts.

Torque and Newton’s 2^nd Law of Motion

In dynamic systems, torque is related to Newton’s 2^nd Law for Rotational Motion. It plays a critical role in determining angular acceleration. It is given as,

$\vec{\tau} = I \cdot \vec{\alpha}$

Here,

$I$ = moment of inertia of the body
$\alpha$ = angular acceleration

Note that, moment of inertia and angular acceleration in the rotational motion are the analogues to mass and acceleration, respectively, in the linear motion.

Torque vs Angular Acceleration

For a body at rest, the angular acceleration is zero, and hence the torque is zero.
For a body moving with uniform angular speed, the angular acceleration as well as the torque is zero.

Applications of Torque in Engineering Devices

Robotics: Torque governs the movement of robotic arms and joints.
Rotating Machinery: From turbines to electric motors, torque is a key parameter.
Automobiles: Torque is essential in engine design, influencing acceleration and towing capacity.
Mechanical Tools: Devices like wrenches and screwdrivers rely on torque to function effectively.
Sports Equipment: Torque impacts the performance of equipment such as golf clubs and bicycles.

Conclusion

Torque is more than just a theoretical concept. It is an integral part of daily life and technological advancements. From simple tools to complex machinery, the principles of torque take part in countless applications.

Understanding torque not only enhances our grasp of physics but also paves the way for innovations in engineering and beyond.

Frequently Asked Questions (FAQs)

What is torque in physics?

Torque is the measure of the tendency of a force to rotate an object about an axis, fulcrum, or pivot. It can be calculated as the product of the force and the perpendicular distance (moment arm) from the axis of rotation.

What are the key components of torque?

The key components are the force applied, the moment arm (perpendicular distance from the pivot to the line of action of the force), and the angle between the force vector and the moment arm.

What is the SI unit of torque?

The SI unit of torque is the Newton-meter (Nm).

How is torque different from force?

Force initiates linear motion, while torque induces rotational motion. Force acts in a straight line, whereas torque is the rotational influence of a force about an axis.

What is the right-hand rule in torque?

The right-hand rule helps determine the direction of the torque vector: point your fingers along the moment arm, curl them in the direction of the force, and your thumb will indicate the direction of the torque.

What are the conditions for zero torque?

Torque becomes zero if either (or all) of the conditions are satsified:

The moment arm ( $r$ ) is zero.
The applied force ( $F$ ) is zero.
The angle between the force and the moment arm is zero ( $\sin\theta = 0$ ).

How is torque calculated mathematically?

Torque can be calculated using the formula:

$\tau = r \cdot F \cdot \sin\theta$

Here, r is the moment arm, F is the applied force, and $\thetaθ$ is the angle between the force and the moment arm.

What are some practical applications of torque?

Torque is used in various applications, including:

Engine performance in automobiles.
The operation of mechanical tools like wrenches.
Rotating machinery like turbines and motors.
Robotics for moving joints and arms.

How does torque relate to Newton’s second law of motion?

Torque relates to Newton’s second law in rotational motion as:

$\tau = I \cdot \alpha$

Here, $\tau$ is torque, $I$ is the moment of inertia, and $\alpha$ is angular acceleration.

What is the difference between torque and moment?

While closely related, torque typically refers to the rotational effect in dynamic systems, whereas a moment often describes bending or twisting effects in static systems, such as in structural analysis.

Table of Contents

Introduction

Torque

Key Terms Associated With Torque

Pivot (or Axis of Rotation)

Force and the Pivot

Moment Arm

Force and the Moment Arm

Rigid Body

Key Properties of Torque

Representation

Unit

Type of Quantity

Nature of Quantity

Direction of Torque

Right-Hand Rule

Mathematical Formulation

Determination of Torque by Resolving Force

Determination of Torque by Resolving Moment Arm

Torque as a Cross-Product

Magnitude of the Torque

Maximum Torque

Zero Torque

Torque vs. Force

Torque vs. Moment

Torque and Newton’s 2nd Law of Motion

Torque vs Angular Acceleration

Applications of Torque in Engineering Devices

Conclusion

Frequently Asked Questions (FAQs)

What is torque in physics?

What are the key components of torque?

What is the SI unit of torque?

How is torque different from force?

What is the right-hand rule in torque?

What are the conditions for zero torque?

How is torque calculated mathematically?

What are some practical applications of torque?

How does torque relate to Newton’s second law of motion?

What is the difference between torque and moment?

Leave a Comment Cancel Reply

Torque and Newton’s 2^nd Law of Motion