Learning how to translate word problems into simultaneous linear equations (SLEs) is very important both in the field of mathematics and engineering. Here, we shall see its definition, and five effective methods to find the solution of these simultaneous linear equation in a generic format.

Introduction

Simultaneous Linear Equations (SLEs) play a crucial role in solving problems where multiple conditions need to be satisfied at the same time.

From simple real-life problems like mixing solutions and/or age problems to advanced applications in engineering and economics, SLEs offer a systematic way to find unknown variables. There are five different methods to solve these equations.

What Are Simultaneous Linear Equations (SLEs)?

Simultaneous Linear Equations refer to a set of two or more equations involving the same variables, where all equations must be satisfied simultaneously. The general form of SLEs in two variables can be written as:

   

   

Here, x and y are the variables, and a₁, b₁, a₂, b₂ are coefficient, and c₁, c₂ are constants. The goal is to find values of x and y that satisfy both equations and is called as the solution of simultaneous linear equations.

For the case where three variables are involved, the general form of SLEs is given as follows:

   

   

   

Why Solving SLEs is Important?

Solving SLEs helps in various real-world scenarios such as:

• Optimising resource allocation in business.
• Understanding intersection points of lines in geometry.
• Analysing systems of equations in economics and statistics.
• Solving physics and engineering problems involving multiple forces or constraints.

5 Effective Ways to Solve Simultaneous Linear Equations

There are different ways to solve a system of SLEs. However, only the five most fundamental are discussed here.

These methods are included in the curriculum from 6^th or 7^th class (grade) through higher secondary school. In higher secondary schools, it covers 9^th and 11^th grades, in simpler terms, matriculation and intermediate studies, as well as IGCSE, or we can say, O–Level, and A–Level courses).

The five methods for the solution of SLEs are listed below. To know more about these methods, click here.

1. Graphical Method
2. Substitution Method
3. Elimination Method
4. Cross Multiplication Method
5. Matrix Method

5 Common Mistakes and How to Avoid Them

While converting the word problems, below are the mistakes that hinder the solution of simultaneous linear equations.

Misinterpreting Keywords

The most basis mistake, among starters, is confusing phrases like “decreased by” and “less than.”

Solution

Familiarise with common phrases and practice to translate them into mathematical symbols.

Inexpertness to Define Variables

The opening of the question is to define variables. But, most of learners fail due to lack of understanding about how to determine and assign clear variables for unknowns.

Solution

The most optimal approach is to read different problem statements. Try to define which variable(s) involved in the problem and what each of them represents before writing the equation.

Incorrect Operation Selection

It means to be unable to judge the operation involved, meaning, using addition when the problem indicates subtraction, and/or vice versa.

Solution

Carefully read the problem and always double-check the corresponding operations.

Forgetting About Order of Operations

This problem is mostly observed with those that lacks basic understanding of arithmetic operations. They ignore the correct sequence when multiple operations are involved.

Solution

For starters, the first and foremost is to pay complete attention while solving question and avoid distraction of thoughts. Afterwards, use correct order of operations in complex equations which usually follows either of the two;

• BODMAS (stands for brackets, orders (powers and roots), division, multiplication, addition, and subtraction)
• PEMDAS (stands for parentheses, exponent, multiplication, division, addition, and subtraction)

The two acronyms serve exactly the same function, the only difference lies on the regional educational practices. For instance, the former is used in the UK and countries that were once part of the British Empire. On the other hand, the latter is used in the US.

Overcomplicating Simple Problems

One of the most common issue, among all group of people, is to try to apply complex methods to straightforward problems.

Solution

Read the statement carefully and filter out the unnecessary details and simplify the problem by focusing on the essential elements only.

Converting Word Problems into Mathematical Equations

Translating word problems into mathematical equations is a crucial skill in mathematics. This process involves identifying the mathematical operations that correspond to the phrases used in the problem and converting them into algebraic expressions.

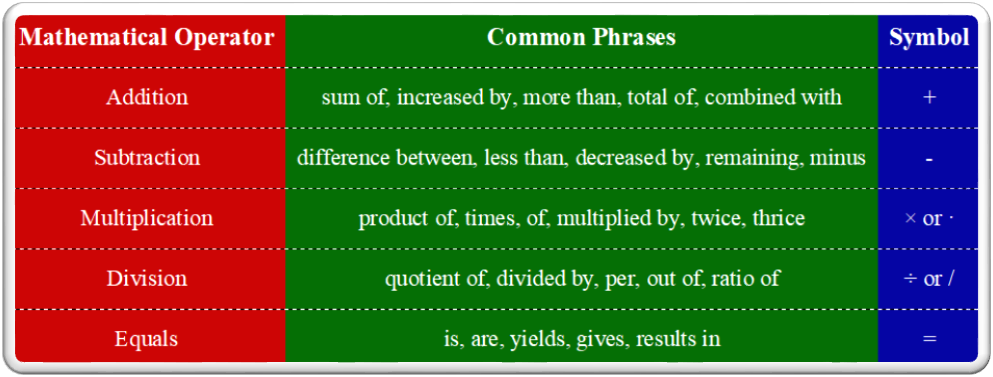
Common Phrases and Corresponding Mathematical Symbols

Here, we can see some common phrases used in word problems, along with their corresponding mathematical operators and symbols.

5 Steps to Translate Word Problems into Simultaneous Linear Equations

Read the Problem Carefully

Understand the context of the problem and what is being asked.

Identify Keywords or Phrases

Look for keywords or phrases that indicate mathematical operations.

Assign Variables

Define variables to represent unknown quantities. Prefer to use first letter (or the most prominent letter) of the quantities or parameters involved.

Translate Phrases into Equations

Use the identified keywords or phrases and variables to state conditions (formulate equations). There could be as many conditions as the number of variables involved.

Review the Equation

Ensure that the equation accurately represents the problem, meaning translation of English language to mathematical language has smoothly achieved.

Conclusion

Simultaneous Linear Equations form the foundation of many mathematical and real-life applications. Mastering the five methods to solve SLEs provide us a multipurpose toolkit for solving different types of problems.

These methods include; graphical method, substitution method, elimination method (also called as equating coefficient method), cross–multiplication method, and matrix method (both inverse method and Cramer’s rule).

Each method has its strengths, and the choice of which to use depends on the complexity and context of the problem.

With these methods, solving SLEs becomes more natural. It is because, it makes it easier to understand the relationships between variables and their practical applications.

Frequently Asked Questions (FAQs)

What are simultaneous linear equations?

Simultaneous linear equations are a set of two or more equations with the same variables, where all equations must be satisfied at the same time.

Why are simultaneous linear equations important?

They are essential for solving real-world problems, including resource optimisation, geometry, economics, and engineering.

What methods can be used to solve simultaneous linear equations?

Common methods include the graphical method, substitution method, elimination method, cross multiplication method, matrix method, and Cramer’s rule.

What are common mistakes when solving SLEs?

Common mistakes include misinterpreting keywords, neglecting to define variables clearly, incorrectly selecting operations, and forgetting the order of operations.

What is the best method to solve simultaneous linear equations?

The best method depends on the problem.

• For simple systems, the substitution or elimination method works well.
• The graphical method is helpful for visual representation but is less precise in providing exact values.
• For more complex problems involving multiple variables or larger systems, the matrix method (including Cramer’s rule and/or inverse method) is more efficient.